Исследование эффективности алгоритмов размещения конструктивных элементов РЭС, страница 2

3. АЛГОРИТМ ПОСЛЕДОВАТЕЛЬНОГО РАЗМЕЩЕНИЯ

Алгоритм включает такую последовательность действий.

1. Сформировать матрицу расстояний D, элементы которой будем определять по формуле ортогональной метрики:

                          d_ij = |x_i - x_j| + |y_i - y_j| .                                                             (3.2)

2. Для каждой строки матрицы D определить суммарное значение:

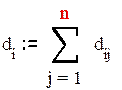3. Ввести матрицу связности R и ее размерность n.

4.Для каждой строки матрицы связности R определить сумму элементов:

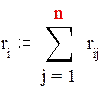5. Найти минимальное значение d_i, если B=i, то пометить столбец j=B.

6. Найти максимальное значение r_i , если Е=i, то удалить столбец j=B.

7. Разместить элемент Е в позицию В.

8. Найти минимум d_i среди оставшихся (m – 1) элементов; просмотреть строку с минимальным d_i и найти минимальный d_ij среди помеченных элементов. Здесь j=B. Определить, какой элемент расположен в позиции j; вновь присвоить B=i, j=B и пометить столбец j.

9. Рассмотреть строку Е в матрице R и найти максимальный r: присвоить E=i, j=E и пометить столбец j.

10. Найти число помеченных столбцов k; если k<n, идти к 8, иначе – к 11.

11. Подсчитать суммарную длину соединений.

4. АЛГОРИТМ ПРЕДВАРИТЕЛЬНОГО РАЗМЕЩЕНИЯ

Алгоритм включает такую последовательность действий [3]:

1.  Для каждой строки матрицы R определить сумму элементов в каждой

7

строке матрицы r_i = S r_ij ,   j = 1,…, n.

j=1

2.  Найти минимум среди r₁,  i = k.

3.  Поместить элемент k в первую по порядку 1,…,n незанятую позицию 1.

4.   В матрице R вычеркнуть k-ю строку, а элементы k-го столбца без вычеркнутого n_k элемента с отрицательным знаком переписать с k-го на 1-е место.

5.  Если число строк в матрице не равно нулю, идти к 2.

6.  Вычислить матрицу расстояний D.

7.  Подсчитать суммарную длину соединения L по формуле (3.1).

Конец.

5.  АЛГОРИТМ ОБРАТНОГО РАЗМЕЩЕНИЯ

Алгоритм включает такую последовательность действий [1, 3].

1.  Вычислить матрицу расстояний D между позициями на плате. Элементы матрицы d_ij определяются по формуле:

d_ij = |x_i  - x_j| + |y_i  - y_j|.

2.  Для каждой строки матрицы D определить суммарное значение элементов d_ij, стоящих в этой строке.

3.  Для каждой строки матрицы R определить суммарное значение элементов r_ij, стоящих в этой строке. Полученные значения – локальные степени элементов.

4.  Упорядочить элементы  t₁ по возрастанию характеристики r_i: t_z1, t_z2, …, t_2n.

5.  Упорядочить позиции l_j по убыванию характеристики d_j : l_d1, l_d2, …, l_dn.

6.  Выполнить размещение элементов в позиции  p(t_k) = l_k, где k = 1, …, n.

7.  Подсчитать суммарную длину по формуле (2.1).

Конец.

Расчетная часть.

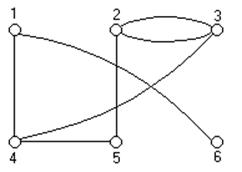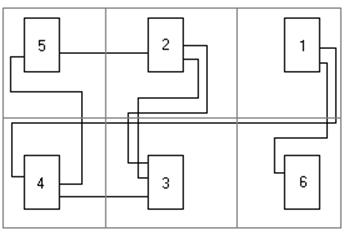
Рис 1.  Схема соединений                                                                         Рис 2. Схема графа.

Дано монтажное пространство, в котором имеется 6 свободных позиций с центрами позиций показанной в таблице.

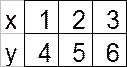
Таблица монтажного пространства.

1.Алгоритм последовательного размещения.

Составим матрицу расстояний D и матрицу связности R. Определим сумму элементов в каждой i-й строке матриц.

                     

Среди  S  d_ij находим минимальное число, оно равно 7 и соответствует позиции  №2. Звездочками помечают

J=1

все элементы  второго столбца матрицы D. Среди  S r_ij  находим максимальное число, оно равно  3 у  вершины  №2.

J=1

Поэтому 2-й модуль, имеющий наибольшее количество связей, размещаем в позицию №2. После этого 2-й столбец матрицы R исключаем из дальнейшего рассмотрения. Имеем

                     

Аналогично получаем

                     

                     

                     

                     

Порядок размещения элементов схемы в монтажном пространстве представлен в следующей таблице.

X – координата центра ячейки по x

Y – координата центра ячейки по y

N – номер элемента

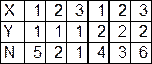
Рис 3.                                                                                              Рис 4.

Преобразованные схемы соединений и графа изображены соответственно на рис.3 и рис.4.

Суммарная длина проводников L=9 у. е.

2.Алгоритм предварительного размещения.

                     

                  

               

Порядок размещения элементов схемы в монтажном пространстве представлен в следующей таблице.

X – координата центра ячейки по x

Y – координата центра ячейки по y

N – номер элемента

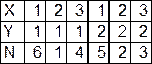
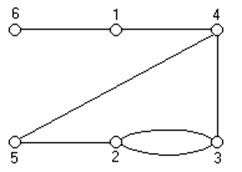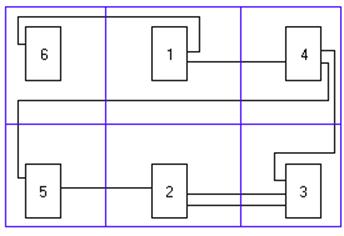
Рис 5.                                                                                              Рис 6.

Преобразованные схемы соединений и графа изображены соответственно на рис.5 и рис.6.

Суммарная длина проводников L=9 у. е.

3.Алгоритм обратного размещения.

                     

Упорядочим Sri по возрастанию:

1(6)  2(5)  2(1)  3(4)  3(2)  3(3)

Упорядочим Sdi по убыванию:

9(1)  9(3)  9(4)  9(6)  7(5)  7(2)

Порядок размещения элементов схемы в монтажном пространстве представлен в следующей таблице.

X – координата центра ячейки по x

Y – координата центра ячейки по y

N – номер элемента

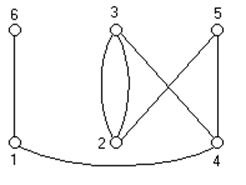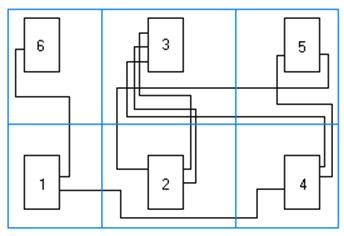
Рис 7.                                                                                              Рис 8.

Преобразованные схемы соединений и графа изображены соответственно на рис.7 и рис.8.

Суммарная длина проводников L=10 у. е.

Вывод: наиболее эффективными оказались алгоритмы последовательного и предварительного размещения.

Суммарная длина проводников L=9 у.е.

Не эффективным оказался алгоритм обратного размещения. Суммарная длина проводников L=10 у.е.