а — входные контакты, эквивалентные действию переключателей, реле, фотоэлектрических датчиков, концевых выключателей и любых других устройств логических систем, формирующих сигнал типа включено/выключено. (Этот символ не следует путать с хорошо известным обозначением конденсаторов в электрических схемах); б — выходные нагрузки — двигатели, клапаны, устройства сигнализации, звонки, лампы, исполнительные механизмы или любая другая электрическая нагрузка, управляемая логической системой; в — логическая инверсия входа, соответствующая оператору НЕ; г — входные контакты, соединенные последовательно, соответствующие оператору И (реализуется выражение А*В); д — входные контакты, соединенные параллельно, соответствующие оператору ИЛИ (реализуется выражение А + В)
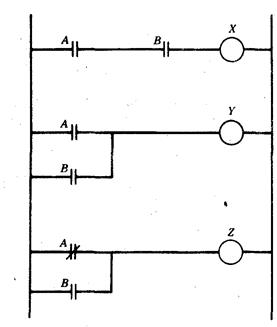
Пример лестничной логической схемы
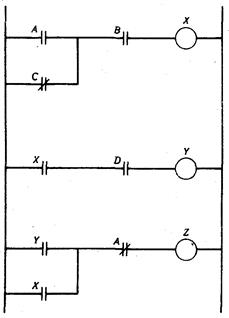
Рис. 11.9
Пример лестничной схемы, в которой состояние выходной нагрузки используется как входной контакт на другой ступеньке лестницы
Правый поручень лестницы отождествляется с нейтральной шиной электрической цепи. Соответственно, контакты (переключатели) принято располагать в левой части схемы, а нагрузки — в правой части, непосредственно у нейтральной шины. Очевидно, каждая простая или составная ступенька лестницы обязательно должна содержать выходную нагрузку того или иного вида, соединенную с нейтральной шиной, иначе произойдет короткое замыкание. В сущности, ступенька без нагрузки будет действовать как прямое соединение шины питания и нейтральной шины, что приведет к срабатыванию плавкого предохранителя или тепловой защиты выключателя.
Наиболее трудным для понимания свойством лестничных схем является то, что входные контакты в них могут повторяться столько раз, сколько это необходимо. Это явление проиллюстрировано на рис. П.8, где вход А присутствует в каждой ступеньке лестничной схемы. Эта схема интерпретирует следующие логические выражения:
Х = А*В;
Y=A+В;
Z=А+В.
Еще одним интересным свойством лестничных схем является то, что состояние данной выходной нагрузки (включена/выключена)
может играть роль входной переменной логической системы, и, следовательно, оно может быть отражено в виде входного контакта на другой ступеньке лестничной схемы. Рис. 11.9, иллюстрирующий это свойство, приводит нас к следующим выражениям:
![]()
где ![]() и
и ![]() .
.
В результате подстановки получим
![]()
С помощью теорем булевой алгебры читатель без особого труда сможет упростить выражение для выходной переменной Z, что, в свою очередь, приведет к упрощению лестничной схемы. Предлагаем читателю в качестве упражнения решить эту задачу самостоятельно.
Важно понимать то, что во всех практических случаях логические выражения, соответствующие лестничной схеме, вычисляются одновременно. Порядок ступенек в лестнице не имеет значения, за исключением некоторых случаев применения программируемых контроллеров, как это будет показано в гл. 12. Однако здесь уместно игнорировать некоторые исключения и считать, что все вычисления производятся одновременно, т. е. все ступеньки лестницы как бы являются параллельными ветвями одной и той же электрической цепи.
Если теперь вернуться к самой первой рассмотренной нами лестничной схеме (рис. 11.6), то читатель уже достаточно подготовлен, чтобы узнать в ней логику пульта с блокировкой. Заметим, что для выхода здесь использовано обозначение Р' в противоположность обозначению Р для входа, Это сделано лишь для того, чтобы все обозначения соответствовали логической схеме на рис. 11.1, образованной с учетом правил, изложенных в гл. 10. Однако в лестничных схемах сама их символика достаточно ясно говорит о том, какие элементы являются входными и какие выходными, поэтому нет необходимости использовать «штрих» или другое обозначение переменной, чтобы отличать входы от выходов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.