Графическая интерпретация логических функций (Глава 11 книги "Роботы и автоматизация производства")

11. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ

Промышленные логические системы управления, с которыми мы познакомились в предыдущей главе, удобнее изображать, проектировать и исследовать, пользуясь каким-либо из графических методов. Графическая интерпретация неоценима в тех случаях, когда логическая система становится довольно сложной — а это характерно для большинства прикладных задач автоматизации производства. Промышленные логические системы, как правило, не удается описать только булевыми выражениями. Это затруднение объясняется тем, что в состав реальных систем обычно входят таймеры, запоминающие устройства, счетчики, элементы задержки; с этими устройствами мы познакомимся чуть позже. Данная глава имеет целью дать читателю представление об огромных возможностях логических систем при автоматизации производства. Для студентов и инженеров-практиков она полезна тем, что позволит им самостоятельно приступить к решению прикладных задач, с которыми они сталкиваются, путем создания логических систем управления. Они получат также представление о том, как спроектировать и построить простейшие промышленные роботы из типовых элементов автоматики.

11.1. ЛОГИЧЕСКИЕ СХЕМЫ

Первый графический метод естественным образом вытекает из рассмотренных в гл. 10 булевых выражений, которые интерпретируются в виде логических схем. Логическая схема составляется из элементов, являющихся аналогами операторов И, ИЛИ и НЕ. Например, на рис. 11.1 изображена логическая схема для пульта с блокировкой, рассмотренного в гл. 10. Для удобства восприятия этой схемы еще раз приведено соответствующее логическое выражение и раскрыт смысл логических переменных. Для многих не составит труда расшифровать обозначения элементов схемы на рис. 11.1, сравнив ее с логическим выражением.

На рис. 11.2 приведена расшифровка обозначений элементов логических схем. В дополнение к этим символам для изображения специальных элементов можно просто использовать квадрат с указанием внутри него функций элемента, например «Таймер» (TMR), «счетчик» и т. п. Кроме символов, принятых в данной книге, на рис. 11.2 приведены также иные обозначения, встречающиеся на практике.

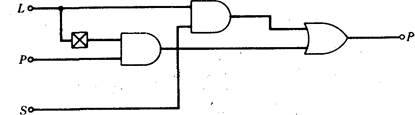
Рис. 11.1

Логическая схема для пульта с блокировкой:

 где L — состояние блокировки; Р — состояние процесса; S - состояние переключателя

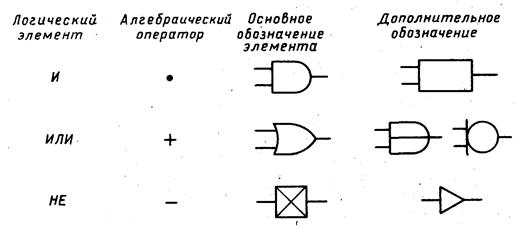
Рис. 11.2

Обозначения элементов логических схем

Логическую схему удобнее всего представлять как некоторую электрическую цепь, входные и выходные сигналы которой суть напряжения. Проводя такую аналогию, однако, следует помнить, что эти напряжения могут принимать только два значения (уровня) в соответствии с двоичной природой логических систем.

На схемах, подобных рис. 11.1„ принята условность, когда черной точкой указывается соединение линий связи, а отсутствие черной точки говорит о том, что пересекающиеся линии не соединены друг с другом. (Черная точка предполагает наличие пайки в месте соединения). По другой версии, все пересекающиеся линии считаются соединенными, а отсутствие соединения обозначается небольшой полуокружностью (рис. 11.3). Вариант, представленный на рис. 11.1, является более предпочтительным.

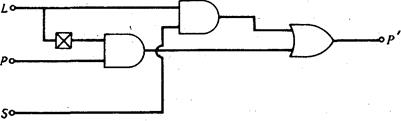
Рис. 11.3

Вариант изображения логической схемы для пульта с блокировкой

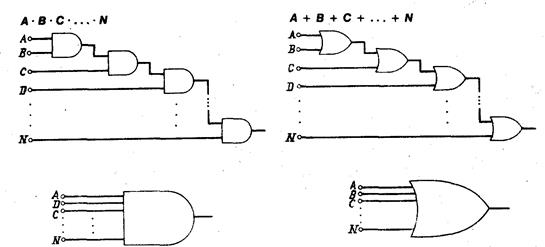
Рис. 11.4

Эквивалентная замена цепочки двухвходовых логических, элементов одним n-входовым

Логический оператор И, связывающий несколько входных переменных, схематически можно изобразить с помощью цепочки двухвходовых элементов И. Однако ту же функцию можно реализовать, используя один n-входовый элемент И. В равной степени это относится и к элементам ИЛИ. Подобная эквивалентная замена показана на рис. 11.4.

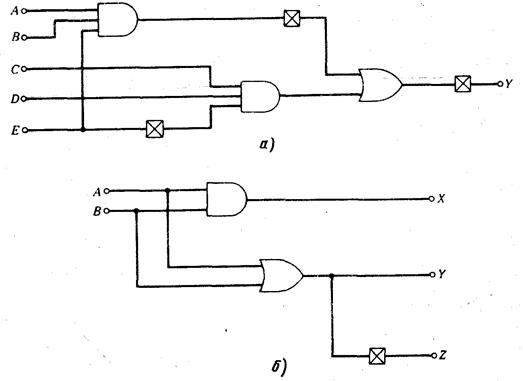
Гис. 11.5

Логические схемы, реализующие следующие булевы выражения:

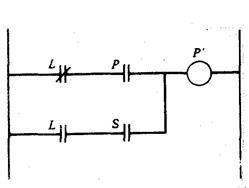
Рис. 11.6

Пример лестничной  логической схемы

В качестве еще одной иллюстрации использования логических cxeм для интерпретации булевых выражений на рис. 11.5 приведены две схемы и соответствующие им выражения. Заметим, что с помощью одной логической схемы на рис. 11.5, б реализованы несколько логических выражений.

11.2. ЛЕСТНИЧНЫЕ ЛОГИЧЕСКИЕ СХЕМЫ

Логические схемы, возможно, являются  наиболее простой и естественной интерпретацией булевых логических выражений, но они не настолько хорошо знакомы специалистам-практикам. Для них более понятен язык лестничных логических (релейно-контактных) схем; этот язык, кстати, характерен для программируемых контроллеров, которые будут рассмотрены в гл. 12.

Преимущество лестничных логических схем заключается в том, что оператор И в них представляется последовательным, а оператор ИЛИ — параллельным соединением элементов (контактов). В простейшем примере на рис. 11.6 схема имеет только одну (или, может быть, две) ступень, но отдаленное сходство с лестницей все же налицо. Если читатель еще не догадался, то скажем, что эта схема соответствует уже знакомому нам примеру с пультом с блокировкой. Чтобы понять, чем отличается язык лестничных схем от языка обычных логических схем, достаточно сравнить рис. 11.6 с рис. 11.1.

Основными элементами лестничной логической схемы являются контакты (входы) и нагрузки (выходы). На рис. 11.7 представлены обозначения этих элементов и показано, как они изображаются в лестничных схемах. Левый поручень лестницы на схеме отождествляется с шиной  электрической  цепи, находящейся под напряжением (обычно 127 В переменного тока, но для большинства логических схем это напряжение намного ниже).

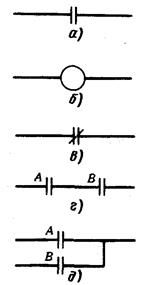
Рис. 11.7

Обозначения элементов лестничных логических схем: