Специфика металлических жидкостей, страница 5

Некоторые металлы имеют аномальное поведение. При плавлении их сопротивление наоборот уменьшается (Sb, As, Bi). Двухвалентные металлы (Zn, Cd) ведут себя аномально в отношении температурного коэффициента. Их удельное сопротивление ρ вначале немного падает, имеет широкий минимум, а при более высоких температурах расплава вновь возрастает.

Щелочные металлы при не слишком высоких температурах имеют положительное значение температурного коэффициента электросопротивления , и их удельное сопротивление вначале после плавления линейно возрастает с увеличением температуры. Электросопротивление некоторых жидких металлов показано в таблице 5.

Таблица 5 – Электросопротивление жидких металлов

При обсуждении поведения  жидких металлов возникает вопрос: можно ли считать приемлемой для расплава концентрацию свободных электронов? Теорией электропроводности в жидких металлах вводится понятие «псевдопотенциал», который описывает суммарный эффект воздействия ядра и внутренних электронных оболочек на электронопроводимость.

Для случая свободных электронов:

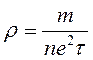,                                          (31)

где n – число электронов в единице объема;

τ – характеристическое время релаксации, равное промежутку между двумя актами рассеяния электрона и связанное с длиной свободного пробега электрона – λ, равной:

,                                             (32)

где υ_F – скорость электрона на уровне Ферми,

m – общее число свободных электронов.

Удельное сопротивление жидких сплавов.При неограниченной растворимости компонентов друг в друге, в твердом состоянии у твердых сплавов закономерности изменения удельного сопротивления подчиняются правилу Нордгейма:

 ~        

 ~                                                  (33)

Правило Матиссена выполняется для большинства разбавленных металлических расплавов и имеет следующий вид:

,                                  (34)

где  – полное сопротивление металла, содержащего примесь;

– сопротивление чистого металла, зависящее от температуры;

 – остаточное сопротивление, не зависящее от температуры и определяющееся типом примеси и ее концентрации.

Влияние примесей на удельное сопротивление.Фактически взаимодействие между атомами примесей в разбавленных растворах может быть исключено, и атомы примеси являются независимыми друг от друга центрами рассеяния электронов. Мотт рассмотрел задачу рассеяния электронов примесями в твердых одновалентных металлах. При этом предполагалось следующее.

1.   Рассеиваемый электрон является свободным так, что эффективное сечение рассеяния на примеси целиком зависит от области действия и вида потенциала, Вызванного примесью.

2.   Рассеяние, вызванное упругой деформацией кристаллической решетки, вблизи примесного атома, пренебрежимо мало.

3.   Концентрация примеси невелика.

4.   Рассеяние на ионах примесей не когерентно, т.е. примеси действуют как независимые точечные силовые центры.

Длина свободного пробега электрона, обусловленная рассеянием на атомах примеси учитывается уравнением:

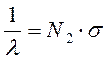,                                                         (35)

где  – атомная доля примеси;

s – эффективное сечение рассеяния электронов на данном сорте примесных атомов.

Дополнительное сопротивление, обусловленное присутствием примеси равно:

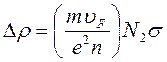.                                                                       (36)