Специфика металлических жидкостей, страница 3

При диффузии возникает поток вещества, стремящийся уменьшить градиент концентрации. Поток исчезает, когда расплав становится однородным. Величина потока   определяется выражением:

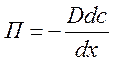,                                              (15)

где  – градиент концентрации какого-либо компонента в расплаве;

 – коэффициент диффузии данного компонента, [см²/с].

Коэффициент диффузии является единственной физической характеристикой скорости выравнивания концентрации данного компонента в расплаве данного состава. Он не зависит от величины градиента.

Для коэффициента диффузии Эйнштейн в своей теории броуновского движения получил выражение:

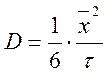,                                                         (16)

где  – средний квадрат величины отдельных перемещений диффундирующей частицы;

 – время между двумя отдельными перемещениями частицы.

Температурная зависимость коэффициента диффузии равна

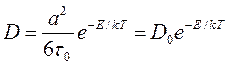,                                     (17)

где  – расстояние между атомами в жидкости (величина среднеквадратичного смещения диффундирующего атома);

 – энергия активации диффузии, равная:

,                              (18)

где , ,  – изменение свободной энергии, энтальпии и энтропии соответственно.

Уравнение коэффициента диффузии имеет следующий вид:

.                                (19)

Подробно вопросу диффузии в твердом состоянии будет уделено в главе 5.

Уравнение вероятности диффузионного перемещения частицы, как в твердом, так и в жидком состоянии имеет вид:

,                           (20)

где ν₀=10^-13-10^-14 с^-1 – частота колебаний атомов вблизи положения равновесия.

Для количественного описания диффузии имеется несколько попыток.

Теория свободного объема Кохина и Тернбала.. В этой теории каждый атом жидкости рассматривается в виде жесткого шара, заключенного в тесное помещение, сформированное его ближайшими соседями. Флуктуации плотности, сотрясающей это помещение, создают в нем зазоры, достаточные, чтобы оказалось возможным диффузионное перемещение центрального атома. Уравнение коэффициента диффузии:

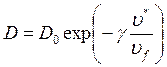,                                               (21)

где υ_f – свободный объем жидкости, рассчитываемый как увеличение объема при плавлении и увеличение объема за счет расширения от температуры;

   – критический объем – это объем, при котором диффузионное перемещение возможно только при образовании рядом с диффундирующим атомом необходимой пустоты;

 и γ – постоянные.

Теория Коледова.В теории Коледова предложена формула для расчета коэффициентов самодиффузии в простых металлических жидкостях по величине флуктуации.

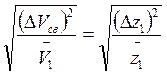                                                (22)

где  – среднеквадратичная флуктуация свободного объема внутри первой координационной сферы произвольно выбранного атома;

 – среднеквадратичная флуктуация валентности атомов металла-растворителя.

На рисунке 31 изображена модель теплового движения в жидких металлах.

Если считать, что зародышем флуктуации является пора, образованная атомами 1, 2, 3, а также атомами, расположенными внизу и поверх этой поры, относительно плоскости чертежа, то эти атомы отодвинуться одновременно на расстояние х от центрального атома 1. Последний окажется расположенным рядом со свободным объемом, который он может занять, передвинувшись вправо на расстояние равное х.

Теория Свелина..

Эта модель предусматривает, что среднеквадратичная флуктуация расстояния между атомами в жидком металле

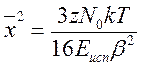     ,                                 (23)

   где z – координационное число,

N₀ – число Авогадро,

k – постоянная Больцмана,

Е_исп – теплота испарения,

β – постоянная.

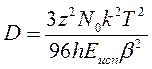,                              (24)

где h – постоянная Планка.

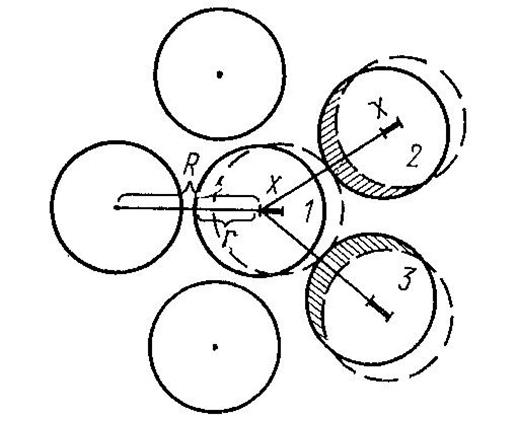
Рисунок 31 – Модель теплового движения в жидких металлах

Температурная зависимость коэффициента диффузии в жидких металлах.Вопрос об этом окончательно не решен – это вопрос дискуссии. Принято считать, что коэффициент диффузии в жидких металлах растет с увеличением температуры по экспоненциальному закону:

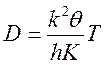,                                               (25)

где  – характеристическая температура;