Вычислить величины дебаевского радиуса и плазменной частоты. Вычислить ларморовский радиус. Вычислить плотность плазмы, если температура электронов равна 5 эВ, страница 3

Некоторые формулы физики плазмы

	Система СИ	СГС (Гауссова)	Расчетная формула при
Плазменная частота ,
Электронная циклотронная частота,
Дебаевский радиус,
Ларморовский радиус,
Альфвеновская скорость,
Скорость ионного звука,
Скорость дрейфа
Отношение давлений (кинетического к магнитному),
Тепловая скорость электронов,
Частота электрон-ионных столкновений,
Частота электрон-электронных столкновений,
Частота ион-ионных столкновений
Средняя длина свободного пробега,

Ответы и решения к некоторым задачам

Глава 1.

Глава 2.

2.1

, следовательно, 20кэВ. миллионам градусов K.

2.4.

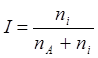Степень ионизации . Концентрация электронов определяется основной компонентой плазмы, поэтому для примеси ее можно считать заданной. Тогда, имея в виду заданную константу равновесия ионизации.

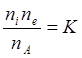, получаем .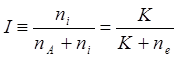

Для основной компоненты концентрация электронов определяется равновесием ионизации. При однократной ионизации . Тогда из соотношения равновесия следует . Если степень ионизации велика, то следует исходить из заданности начальной концентрации атомов . Тогда или 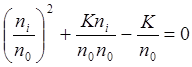. Взяв положительный корень этого квадратного уравнения, получаем выражение для степени ионизации:

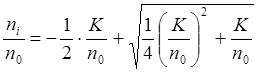
Если степень ионизации мала, то  и , откуда .

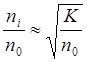2.5.Найти температурную зависимость равновесной концентрации электронов для слабоионизованной плазмы, имеющей потенциал  ионизации основной компоненты J.

Из результата предыдущей задачи следует, что для слабоионизованной плазмы . По формуле Саха видно, что константа равновесия зависит от температуры следующим образом

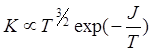
При малой степени ионизации можно пренебречь статистическими весами возбужденных состояний и учитывать только статвеса основных состояний (которые от температуры не зависят). При этом

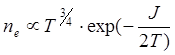
2.6

Приравнивая скорости ионизации электронами и рекомбинации парными столкновениями с излучением: , имеем:

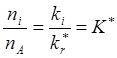. Величина  здесь уже не может быть найдена из термодинамики. Она определится сечениями процессов ионизации и рекомбинации. Стационарное состояние ионизации не зависит от концентрации электронов. Степень ионизации выразится соотношением:

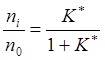 , в которое не входит концентрация электронов. Это не зависит от того, является ли вещество малой примесью или это основная компонента плазмы.

Глава 3.

3.8.

Чтобы частицы плазмы не уходили сразу на стенку установки, их ларморовский радиус должен быть существенно меньше характерного поперечногоразмера системы (в данном случае – диаметра установки. Таким образом имеем условие:

, кторое, после подстановки выражения для ларморовского радиуса, запишется (с точностью до множителя, порядка единицы):

 

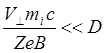
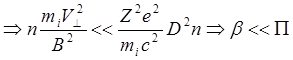
Где - отношение газокинетического давления плазмы (плотность тепловой энергии) к магнитному; - погонное число частиц 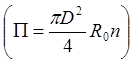, R₀=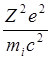 - так называемый классический радиус частицы, определяемый из условия равенства кулоновской энергии частицы и ее собственной энергии .

3.9.

Выпишем нужное нам уравнение Максвелла с учетом тока смещения: 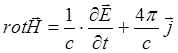, выразим из него  и подставим в (2.2.21). Получим:

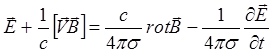. Взяв ротор от обеих частей равенства и учитывая, что , получим уточненное уравнение диффузии магнитного поля:

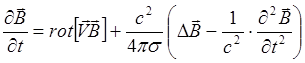 вместо прежнего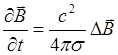

3.10.

Указание

Покидают систему частицы, у которых в центральной части ловушки питч-угол орбиты меньше значения, определяемого соотношением:

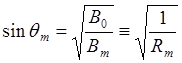. В интересующем нас случае R_m=4, следовательно, в ловушке останутся частица с питч-углами, синус которых превышает

Глава 4.

Глава 5.

Глава 6.

6.3.

Пороговая скорость должна быть больше значения, полученного для холодных ионов. Важна величина объемного заряда, создаваемого ионной компонентой, а следовательно – пролетной плотности ионов. Ионы, имеющие скорости большие средней, дают меньший вклад в пролетную плотность, чем относительно медленные ионы. Разброс в сторону меньших скоростей сильнее увеличивает пролетную плотность, чем уменьшает ее разброс в сторону больших скоростей. Это должно быть скомпенсировано большей средней скоростью.