Записывая
в выражении (1.10) вместо дифференциалов соответствующие производные по ![]() , получаем:
, получаем:
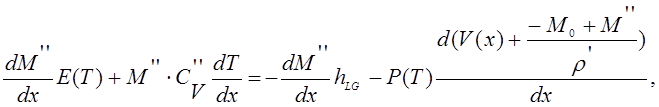 (1.11)
(1.11)
где
x- вертикальная
координата, отчитываемая от головки цилиндра, V(x)
– текущий рабочий объем в зависимости от положения поршня, ![]() - начальная масса
пара фреона,
- начальная масса
пара фреона, ![]() - плотность жидкой фазы фреона.
- плотность жидкой фазы фреона.
Масса газовой фазы определяется соотношением:
![]() (1.12)
(1.12)
Учитывая,
что  ,
,
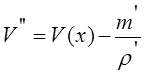 ,
,![]() ,
подставляя
в (1.12) получаем:
,
подставляя
в (1.12) получаем:
 ` (1.13)
` (1.13)
Слагаемым
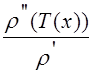 в дальнейшем можно пренебречь, т.к.
плотность жидкой фазы на 3 порядка больше газовой.
в дальнейшем можно пренебречь, т.к.
плотность жидкой фазы на 3 порядка больше газовой.
Подставляем (1.13) в выражение (1.11), упрощаем и приводим дифференциальное уравнение первого порядка к следующему виду:
 (1.14)
(1.14)
здесьF – площадь поршня.
Поскольку кривая насыщения низкокипящих рабочих тел в области совершения работы сильно напоминает изоэнтропу, имеет смысл, вдобавок, рассчитать параметры пара по уравнению изоэнтропы:
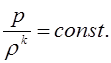 (1.15)
(1.15)
Зависимость давления от положения поршня будет определяться соотношением:
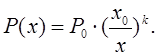 (1.16)
(1.16)
Зависимость температуры от положения поршня будет определяться соотношением:
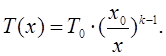 (1.17)
(1.17)
Глава 2. Расчет энергетической установки на фреоне 141b.
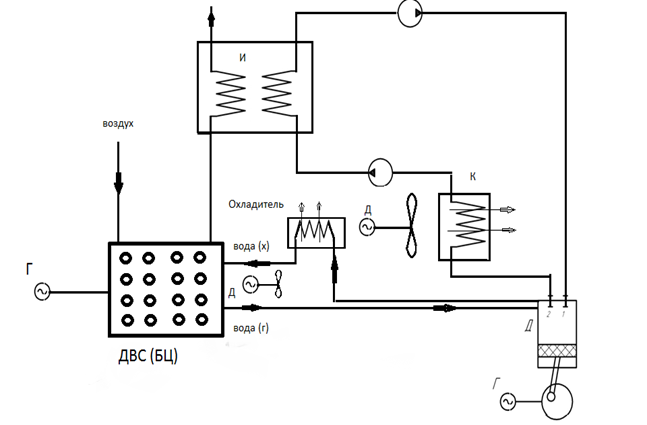
Рис. 2.1 Принципиальная схема установки на фреоне 141b.
Параметры данной установки:
![]() °С – температура выхлопных газов
на входе в испаритель,
°С – температура выхлопных газов
на входе в испаритель,![]() °С – температура выхлопных газов
на выходе из испарителя,
°С – температура выхлопных газов
на выходе из испарителя,![]() °С – температура фреона 141b
на входе в испаритель,
°С – температура фреона 141b
на входе в испаритель, ![]() °С – температура фреона 141b
на выходе из испарителя,
°С – температура фреона 141b
на выходе из испарителя, ![]() давление фреона на входе в конденсатор,
давление фреона на входе в конденсатор,
![]() давление фреона на выходе из
испарителя.
давление фреона на выходе из
испарителя.
Основным ограничением для расчета установки на фреоне 141b из-за опасности разложения фреона является температура на выходе из испарителя, равная 180 °С.
2.1 Тепловой расчет пластинчатого испарителя.
Аппарат проектируем на базе пластин “ПР- 0,5Е” из стали Х18Н10Т.
Соответствующие
параметры: ![]() – поверхность теплопередачи одной
пластины,
– поверхность теплопередачи одной
пластины, ![]() м - эквивалентный диаметр
межпластинчатого канала,
м - эквивалентный диаметр
межпластинчатого канала, ![]()
![]() - площадь поперечного сечения
одного канала,
- площадь поперечного сечения
одного канала, ![]() м – приведенная длина канала,
м – приведенная длина канала, ![]() м – диаметр углового отверстия,
м – диаметр углового отверстия, ![]() м – толщина пластины.
м – толщина пластины.
1) По известным нам параметрам составляем уравнение баланса и находим расход фреона:
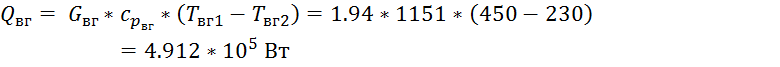
Соответственно
![]() ,
,
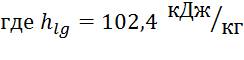
Отсюда
находим расход фреона: ![]()
![]() .
.
2) Вычисляем средний температурный напор:
![]() °С
°С
![]() °С
°С
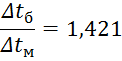
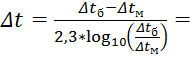 38.64
38.64
3) Определяем скорость движения фреона в канале:
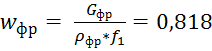
![]()
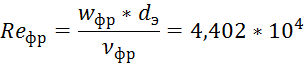
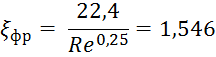
4) Вычисляем
критерий Прандтля ![]() и
и ![]() при средней температуре фреона и
стенки:
при средней температуре фреона и
стенки:
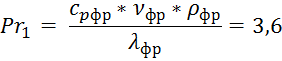
При
![]() °С физические свойства фреона:
°С физические свойства фреона: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
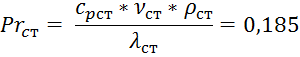
5) Вычисляем критерий Нуссельта со стороны фреона:
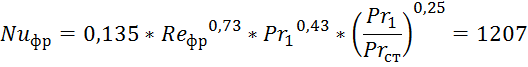
6) Находим коэффициент теплоотдачи от фреона к стенке:
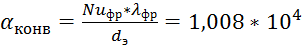
![]()
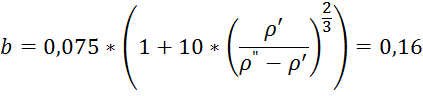
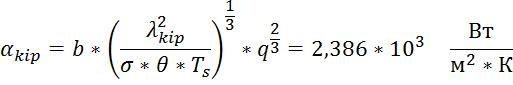
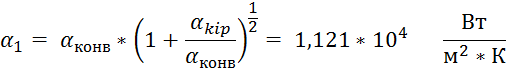
7) Аналогично определяем скорость движения выхлопных газов в канале:
![]()
![]()
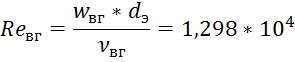
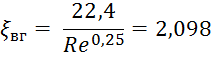
8) Вычисляем
критерий Прандтля ![]() и
и ![]() при средней температуре выхлопных
газов и стенки:
при средней температуре выхлопных
газов и стенки:

При
![]() °С физические свойства выхлопных
газов:
°С физические свойства выхлопных
газов: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
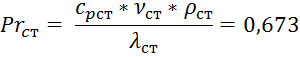
9) Вычисляем критерий Нуссельта со стороны выхлопных газов:
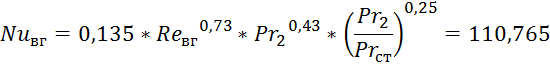
10) Находим коэффициент теплоотдачи от выхлопных газов к стенке:
![]()
![]()
11) Вычисляем коэффициент теплопередачи:
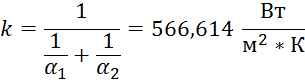
12) Определяем общую поверхность теплопередачи аппарата:
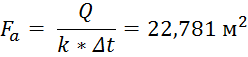
![]()
13) Компоновочный расчет и уточнение величины рабочей поверхности:
а) Площади поперечных пакетов составят:
-
со стороны фреона - 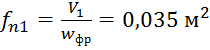 ;
;
-
со стороны выхлопных газов - 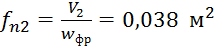 ;
;
б) Число каналов в одном пакете:
-
со стороны фреона - ![]()
-
со стороны выхлопных газов - ![]() ;
;
в) Число пластин в одном пакете:
-
со стороны фреона - ![]()
-
со стороны выхлопных газов - ![]() ;
;
г) Определяем поверхность теплообмена одного пакета при полученном числе пластин:
-
со стороны фреона - ![]()
-
со стороны выхлопных газов - ![]() ;
;
д) Число пакетов в аппарате:
-
со стороны фреона - ![]() ;
;
-
со стороны выхлопных газов - ![]() ;
;
е) Число пластин в аппарате определяем с учетом наличия концевых пластин:
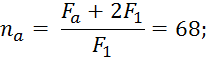
14)
Фактическая
площадь поперечного сечения каналов в пакетах для обеих сред составит: ![]() ;
;
15) Гидромеханический расчет - рассчитаем коэффициент общего гидравлического сопротивления гидравлические сопротивления пластин:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.