Использование дополнительного фреонового цикла на тепле отработанных в двигателе внутреннего сгорания выхлопных газов, страница 8

Благодаря действию этих факторов действительное значение коэффициента теплоотдачи мало зависит от ошибки при выборе предполагаемого значения его, использованного только при расчете скорости.

Это также относится и к возможной погрешности при вычислении средней температуры стенки. Коэффициент сопротивления ξ легко может быть уточнен сразу после получения скорости по числу Рейнольдса, вследствие чего устраняется угроза для точности дальнейшего расчета и необходимость в повторении всего расчета.

При расчете особенно отчетливо выявляется малое влияние точности предварительного выбора величин α,  и ξ, так как значения   (число каналов в пакете для i- ой среды) представляют собой дискретный ряд чисел, и вычисленное по этой формуле значение необходимо в конечном счете округлять до целого числа.

Более того, расчет нередко дает результаты, подсказывающие необходимость применения компоновки с чередующимся числом параллельных каналов в пакетах. Например, при получении в результате вычисления числа 3,45 оказывается целесообразной компоновка с условным 3,5, которая на практике реализуется в виде последовательного соединения пакетов с чередованием числа каналов 3- 4- 3- 4 и т.д.

Также хотелось бы рассмотреть последовательность компоновочного расчета. Компоновочным расчетом теплообменных аппаратов определяется параллельно- последовательная компоновка каналов для каждой рабочей среды.

Например, для пластинчатых теплообменников при расчете определяют: размеры пластин и число каналов в одном пакете; число пластин в каждом пакете и число пакетов в аппарате; общее число пластин в аппарате и основные размеры аппарата.

При компоновочном расчете аппарата используют результаты теплового расчета. Оба вида расчетов являются взаимосвязанными, иногда результаты компоновочного расчета заставляют вносить существенные изменения в тепловой, а также и гидромеханический расчеты.

Порядок компоновочного расчета пластинчатого аппарата следующий:

1.  По заданным расходам рабочих сред и вычисленным или выбранным скоростям их движения в каналах определяют необходимую площадь поперечного сечения пакета:

 ,

-  объемный расход рабочей среды,  ; w – скорость данной рабочей среды,  .

2.  Определяют число параллельных каналов в пакете для каждой среды:

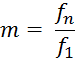
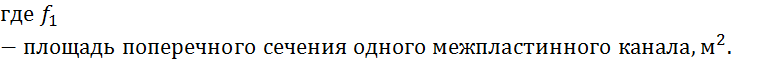
Полученное значение  округляют до целого.

3.  Число пластин в пакете находят по соотношению:

В крайних пакетах, соприкасающихся с плитами, общее число пластин на одну больше (концевую):

4.  Вычисляют поверхность теплопередачи одного пакета:

5.  Определяют число пакетов (ходов) в теплообменном аппарате:

,

 - рабочая поверхность аппарата, найденная при тепловом расчете.

Если величина  получается дробной, то ее округляют до целого числа и корректируют соответственно поверхность всего аппарата:

6.  Находят общее число пластин в аппарате (секции):

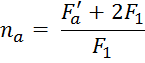
Где  – поверхность теплопередачи одной пластины, .

1.3 Принципиальная методика расчета работы расширения поршневой установки.

Работа расширения  при изменении объема составляет:

(1.1)

здесь – работа, – давление в цилиндре пневмодвигателя, – объём цилиндра.

Первый закон термодинамики имеет вид:

            (1.2)

здесь  – внутренняя энергия,   – количество теплоты.

Изменение энтальпии составит:

 (1.3)

В соответствии с определением внутренней энергии:

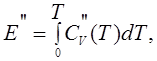 (1.4)

здесь  – внутренняя энергия газовой фазы,  – изохорная теплоемкость паров фреона,  – температура.

Соотношение между энтальпией и внутренней энергией имеет вид:

 (1.5)

здесь – энтальпия газа, – давление газа, – объём газа.

Предполагается, что выделяемое в цилиндре тепло обусловлено конденсацией паров фреона:

                                               (1.6)

здесь – масса жидкой фазы в цилиндре во время рабочего такта,  – удельная теплота парообразования.

Используя соотношения (1.3), (1.6) запишем:

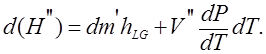                               (1.7)

Используя соотношение (1.4), (1.5):

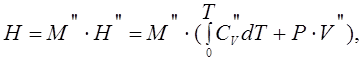                      (1.8)

здесь – масса газовой фазы.

Подставляя (1.8) в (1.7), получаем:

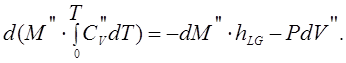                     (1.9)

Берем производную от сложной функции :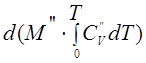

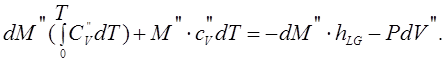                 (1.10)