Критические тепловые нагрузки при кипении, страница 9

Условие превышения плотности теплового потока на стенке значений q_пр конечно же нельзя трактовать как достаточное для достижения термодинамического предела кипения. Имеющиеся опытные данные о КТН при кипении в сильно недогретом прямолинейном потоке в условиях равномерного нагрева, сопровождавшиеся и температурными измерениями [65, 75, 174, 175 и др.], позволяют утверждать, что температуры стенки при кризисе заведомо меньше температур предельного перегрева жидкости Т_пп. Исключением являются область высоких приведенных давлений и значительных скоростей потока, при которых собственно кипение может начинаться при температурах стенки, близких к Т_пп [176]. Выполненное в [177] сопоставление расчетов по (1.14) (с уточненным числовым коэффициентом при равным 11) с данными обобщенных таблиц о КТН для воды [178] для сильно недогретого скоростного потока (rw  > 2000 кг/(м²×с), Т_s–T_ж > 50 K, согласно [90]) показало хорошее соответствие данных. Для меньших недогревов в [177] предложена интерполяционная формула, дающая при больших недогревах и скоростях выражение (1.14), а при Т_ж = T_s формулу для КТН насыщенной жидкости.

Анализ новых данных, в сравнении с использованными в [177], о КТН при кипении в сильно недогретом прямом высокоскоростном потоке, например [65, 91] показывает, что значения, определяемые (1.14), являются, по сути, верхним пределом для плотности теплового потока на стенке. На рис. 6.26 представлено сравнение расчета по (1.14) (выполненного по рекомендациям [90], за Т_ж принята температура на выходе) с опытными данными [65, 91]. Данные [65] представлены точками, полученными в трубе внутренним диаметром d = 0,902 мм, p_вых = 3,1 МПа, Т_вх = 25–26 ^оС, l/d > 10. Данные [91] получены в трубе внутренним диаметром d = 2,5 мм, p_вых = 2.3–2.6 МПа, Т_вх » 30 ^оС, l/d = 40. Из сравнения можно отметить хорошее соответствие значений, рассчитанных по (1.14) опытным данным.

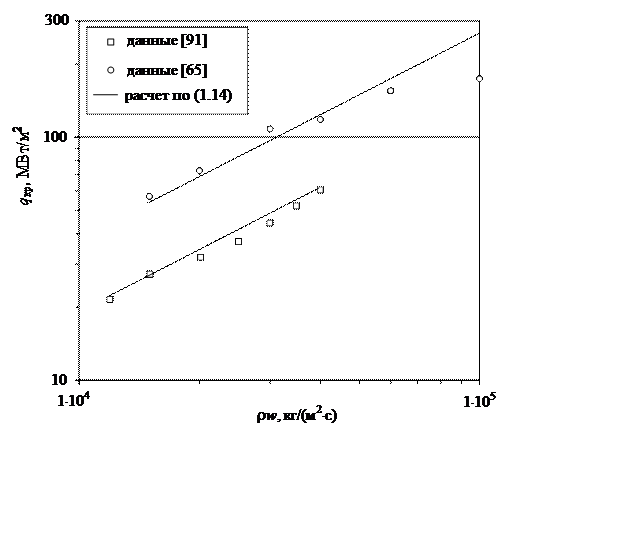
Рис. 6.26. Сравнение расчета по уравнению (1.14) с опытными данными о КТН при кипении [65] и [91]

При кипении в сильно недогретом потоке характерна ситуация, когда значения плотности теплового потока q_пр, рассчитанные с использованием (1.14) по параметрам теплоносителя на входе, заметно превышают значения q_кр (для данных [91], представленных на рис. 6.26 на » 35%). Можно дать следующее объяснение этому обстоятельству. По ходу потока уменьшается давление жидкости и возрастает температура, что приводит к заметному уменьшению значений  q_пр. Наконец, когда своеобразный “запас” отвода тепла в ядро потока вынужденной конвекцией исчерпан, пузырьковый слой на стенке полностью развит, происходит развитие кризисных явлений. Это проявляется в слиянии отдельных пузырей, образовании паровых конгломератов (т.н. бланкета), происходит испарение микрослоя жидкости, потеря контакта жидкости со стенкой, значительный рост в локальной области температуры стенки и ее разрушение. Подробные визуальные исследования развития кризиса в этих условиях, описаны например в [51, 179], где также приведена количественная информация о размерах паровых образований и их эволюции.

Очевидно, что для достижения плотности теплового потока на стенке значений q_пр необходимо сохранить высокие значения недогрева и ограничить возможность развития пузырькового слоя на стенке. Наиболее просто в условиях эксперимента это возможно за счет уменьшения длины трубки. В качестве иллюстрации этого тезиса на рис. 6.27 представлены опытные данные [65] о q_кр в трубе внутренним диаметром  d = 0,902 мм при rw = 15000 кг/(м²×с), p_вых = 1,03 МПа, Т_вх = 23–27 ^оС при значениях относительной нагреваемой длины l/d =6.2, 6.4, 11.6, 17.7, 22.4, 23.9 и 28.5 в зависимости от соответствующей температуры жидкости на выходе. На рис. 6.27 также показаны результаты соответствующего расчета по (1.14).