Критические тепловые нагрузки при кипении, страница 11

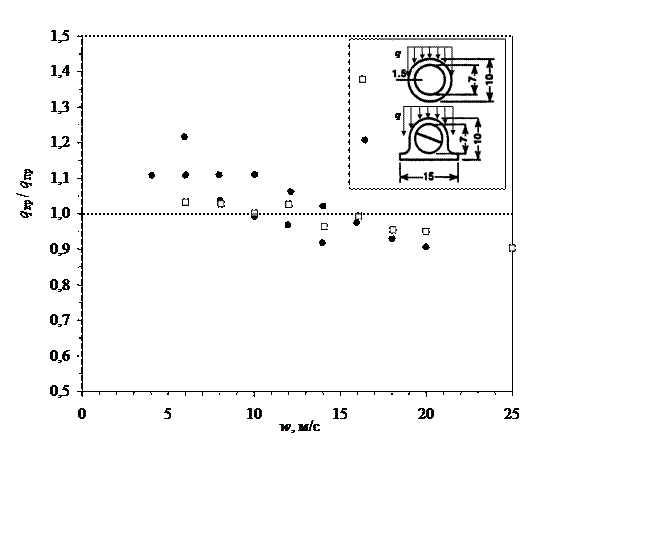
Рис. 6.28. Сравнение опытных данных о КТН [119] с расчетом по (1.14) для прямого потока (□) и по (6.1) для закрученного (·)

Данные, представленные на рис. 6.28 говорят о хорошем соответствии опытных значений КТН [119] расчету по (1.14) для прямого потока и по (6.1) для закрученного. Присутствующее некоторое систематическое изменение отношения  q_кр / q_пр с ростом скорости потока может быть объяснено неучетом при расчете числа Re в (1.14) и (6.1) неизотермичности канала в силу отсутствия в [119] данных о температуре стенки.

Сопоставление результатов расчета по (6.1) с опытными данными о КТН при кипении в сильно недогретом закрученном потоке при неравномерном по периметру нагреве [108] и [106] представлено на рис. 6.29 и 6.30, соответственно. Данные [108] получены при моделировании одностороннего нагрева с использованием разрезной трубы с нагреваемой половиной периметра. Внутренний диаметр труб был 8.0 и 15.0 мм, скорость потока составляла       w = 5.2–15.1 м/с, p_вых = 2.6 – 3.6 МПа, Т_вх = 44–103 ^оС. Данные получены при наибольшем практически реализуемом значении коэффициента закрутки ленты k= 1.57, а также при k= 0.79.

Рис. 6.29. Сравнение опытных данных о КТН [108] с расчетом по (6.1)

Сопоставление, представленное на рис. 6.29, позволяет утверждать, что с учетом разброса данных значения КТН практически не превосходит q_пр. При наибольшем коэффициенте закрутки k= 1.57 вклад второго слагаемого q_ц в (6.1) достигает 30–35% от значения первого слагаемого. Таким образом, в условиях опытов [108] не удается ограничить развитие пузырькового пограничного слоя на стенке. Увеличение q_кр при нагреве половины периметра трубы в сравнении с нагревом всего периметра, в [108] обусловлено поддержанием большего недогрева жидкости.

В отличие от [108] данные [106] получены при моделировании одностороннего нагрева с использованием труб с различной толщиной стенки. Часть периметра трубы с повышенным тепловыделением составляла четверть, половину и три четверти от полного периметра трубы. На рис. 6.30 представлены данные [106] о КТН при rw = 4000 кг/(м²×с), Т_вх » 40 ^оС, k= 0.60 для разных давлений на выходе из РУ.

Рис. 6.30. Сравнение опытных данных о КТН [106] с расчетом по (6.1)

По рис. 6.30 можно отметить влияние неравномерности нагрева на значения КТН. И если при повышенном нагреве ¾ части периметра отличия от условий равномерного нагрева в значениях q_кр не столь заметны, то при уменьшении доли с повышенным тепловыделением  заметно увеличиваются и значения q_кр. К сожалению, в [106] не представлены данные о значениях температуры потока на выходе и о распределении тепловых потоков на стенке с разной толщиной, поэтому, исходя из уравнения теплового баланса, корректно определить значение температуры потока на выходе возможно только для условий равномерного нагрева, для которых на рис. 6.30 показано значение q_пр, рассчитанное по (6.1).

Вместе с тем, оценки показали, что отличия в значениях q_кр для разных условий нагрева опытов [106] не могут быть объяснены различиями в недогреве жидкости. При наименьшей доле с повышенным тепловыделением значения q_кр превосходят q_пр, определяемое по (6.1). В опытах [106], при наименьшей доле с повышенным тепловыделением, условия нагрева наиболее близки к условиям одностороннего нагрева пучками частиц. Данные рис. 6.30 позволяют говорить об ограничении развития пузырькового пограничного слоя на стенке в этих опытах. Авторы [106] провели сравнительный анализ расположения локальной области начала развития кризиса на стенке РУ при разных условиях нагрева, показавший, что инициализация кризиса происходит, как правило, в конце зоны периметра с повышенным тепловыделением вдоль по потоку. Отсутствие в [106] данных о температуре стенки при значениях плотности теплового потока, соответствующих q_кр, не позволяет утверждать о достижении в этих опытах термодинамического предела кипения. Расчет плотности теплового потока по (5.4), выполненный для данных [106] из условия соответствия температуры стенки температуре предельного перегрева жидкости дает значения, превышающие q_кр. Хорошее соответствие результатов расчета теплообмена при кипении по (5.1) для данных о теплообмене этих же авторов [75] (см. рис. 5.17) дает основания полагать, что значения q_кр могут быть рассчитаны по (5.1) по соответствующей температуре стенке Т_кр. Можно отметить, что сами авторы [106] не включают собственные данные для закрученного потока при неравномерном нагреве в обработку при построении методики расчета КТН при кипении в недогретом потоке [103].