Наиболее спорным моментом модели [189] является предположение о том, что касательное напряжение на межфазной поверхности определяется по аналогии с трением потока жидкости на твердой поверхности канала, причем в условиях полностью развитой шероховатости стенки. Шероховатость поверхности пленки связывается с развитием волн неустойчивости Гельмгольца-Кельвина. Указанная задача о неустойчивости относится к невязким жидкостям, неограниченно простирающимся в направлении от границы раздела, т.е. к рассматриваемой геометрии неприменима. Далее, за исключением специфической области околокритических давлений плотность и динамическая вязкость жидкости намного превосходят соответствующие свойства пара. Благодаря сильным неравенствам ρп << ρж, μп << μж обтекание капельной жидкостью газовых включений в большинстве случаев происходит безотрывно, и, во всяком случае, совершенно непохоже на обтекание твердой поверхности. Наконец, в [189] в неявном виде принимается, что поверхность пленки неподвижна относительно стенки канала, что, очевидно, завышает величину поперечного потока импульса и приводит к отсутствию вязкости пара в итоговых соотношениях.
Кроме того предположения [189] о развитой шероховатости на поверхности паровой пленки и о ламинарном течении пара в ней трудно совместимы. При высоких скоростях течения жидкости и высоких приведенных давлениях используемое представление о тонкой паровой пленке с непрерывной границей, отделяющей ее от жидкости, перестают быть адекватными реальной структуре потока. Для воды при давлениях 19,6–21,6 МПа плотности пара и воды отличаются всего в 2-3 раза. При развитой турбулентности можно ожидать, что область перехода от паровой фазы на стенке к жидкой в ядре представляет собой достаточно гомогенную структуру. При этом весьма вероятно, что и на стенке канала существуют локальные участки контакта с жидкостью; это предположение относится, конечно, к условиям небольших средних перегревов стенки по отношению к Ts, характерных для условий работ [190, 191].
Тем не менее, уравнение работы [189] надежно описывает опытные данные о теплообмене при пленочном кипении недогретой жидкости при высоких приведенных давлениях, причем не только воды, но и гелия (данные работы [192] для давления 0,203 МПа). Это следует признать практически важным результатом. Развитый автором [189] подход к задаче о теплообмене при пленочном кипении в турбулентном потоке недогретой жидкости остается единственным, заслуживающим серьезного обсуждения. Как правило, в других работах (например, [174, 197]) модельные представления привлекаются лишь для обоснования структуры безразмерных корреляций, используемых для описания собственных данных.
К сожалению, сопоставление расчетов по уравнению работы [189] с данными [130], представленными на рис. 7.1–7.3 и данными [77, 174, 194–196], показало значительное расхождение (превышение расчетных значений до 5 раз).
Подводя итог рассмотрению опытных данных, для апробации теоретических моделей пленочного кипения в недогретом потоке можно рекомендовать данные [130], [77, 174, 194–196], [198] и [193] при оговоренных выше условиях, полученные при малых и умеренных приведенных давлениях.
7.2. Приближенная модель теплообмена при пленочном кипении в потоке недогретой жидкости
Приближенная модель теплообмена, основана, как и модель работы [189] на использовании аналогии Рейнольдса, и разработана в [209]. Для условий развитого турбулентного течения и больших значений недогрева жидкости до температуры насыщения можно предложить простую предельную модель теплоотдачи при пленочном кипении, схема которой представлена на рис. 7.5.
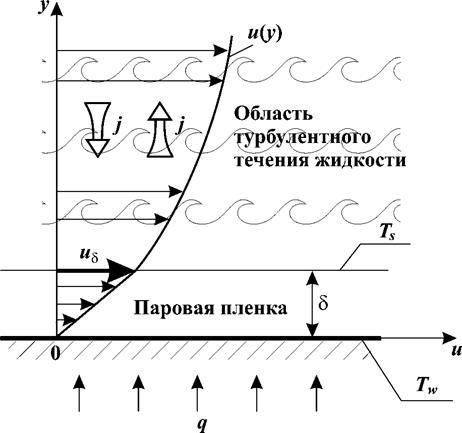
Рис. 7.5. Схема течения и теплообмена через тонкую паровую пленку на стенке
Малая толщина паровой пленки позволяет принять, что в ней абсолютно доминирует молекулярный перенос импульса и энергии, так что на межфазной границе касательное напряжение:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.