Структурный анализ кривошипно-ползунного механизма, страница 2

Среди величин, входящих в уравнения (3.2) переменными являются углы ,  и . Угол  является обобщенной координатой механизма, и поэтому задан. Из уравнений (3.2) подлежат определению переменные  и . Анализ показывает, что эти уравнения сложны для решения. Для упрощения нахождения углов  и  вместо одного сложного контура OABCO рассмотрим два простых OACO и ABCA. Для этого введем в рассмотрение вспомогательный вектор , соединяющий точки A и C. При этом получим:

   (3.3)

            (3.4)

Составим уравнение (3.3) в проекциях на оси координат:

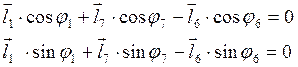  ( 3.5)

Из уравнений (3.5) находим угол наклона вектора

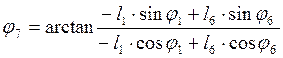  (3.6)

и его модуль

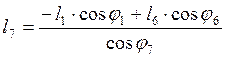  (3.7)

Углы  и  находим из уравнения (3.4), записав его в проекциях на оси координат:

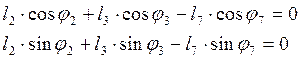   (3.8)

        Слагаемые, содержащие угол , переносим в правые части уравнения, возводим оба уравнения в квадрат и складываем. После преобразования получим:

   (3.9)

Обозначим , откуда

  (3.10)

где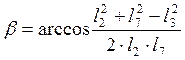. В этих выражениях угол между векторами  и  (рис. 3.3).

Определяем угол  из уравнения (3.8):

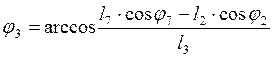   (3.11)

Уравнение замкнутости второго контура имеет вид:

   (3.12)

или в проекциях на оси координат

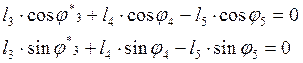   (3.13)

Учитывая, что  и что , тогда из второго уравнения (3.13) находим:  

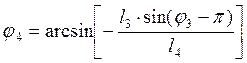
Из первого определяем его модуль:

  (3.14)

Для  определения положения точек  и  записываем уравнения замкнутости контуров  и :      

 (3.15)

  (3.16)

Из уравнения (3.15) и (3.16) находим координаты центров масс звеньев 2 и 4:

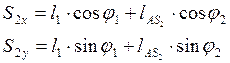  (3.17)

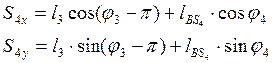  (3.18)

3.4 Определение аналогов скоростей аналитическим методом.

Определение кинематических свойств механизма, когда закон движения начального звена еще не известен, производится с помощью кинематических характеристик, называемых аналогами скоростей, которые не зависят от времени, а являются функциями обобщенной координаты.

Так как аналоги скоростей не зависят от времени, то принимаемрад/с.

Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (3.2) - (3.13). Получим:

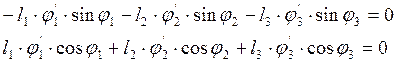 (3.19)

где - аналог угловой скорости звена 1, принимаем , т. к. угловая скорость звена 1 направлена по ходу часовой стрелки;,  - аналоги угловых скоростей звеньев 2 и 3.

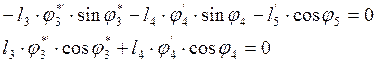 (3.20)

Решая совместно (3.19) находим

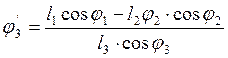  (3.21),

и , вычтя из аргументов всех тригонометрических функций первого уравнения угол :

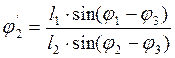  (3.22).

Из второго уравнения (3.20) определяем , так как, тогда

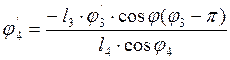  (3.23),

из первого находим проекцию:

  (3.24).

Аналоги скоростей центров масс звеньев 2 и 4 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (3.17) и (3.18):

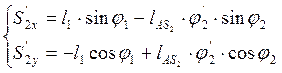 (3.25)

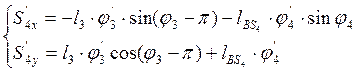  (3.26)

3.5 Определение аналогов ускорений аналитическим методом.

Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (3.19) и (3.20):

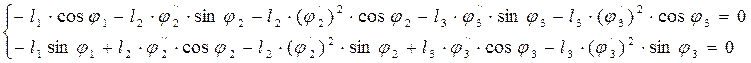(3.27)

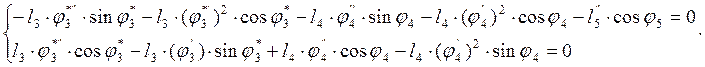(3.28)

В этих уравнениях , ,  - аналоги угловых ускорений звеньев 2, 3, 4;  - аналог абсолютного ускорения ползуна D.

Для определения  и  решаем систему (3.27) обычным методом или, что проще, в первом уравнении системы (3.27) из аргументов всех тригонометрических функций вычитаем угол :

откуда

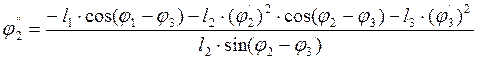  (3.29)

Из второго уравнения определяем

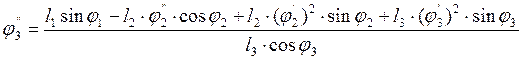  (3.30)

 Из уравнений (3.28) находим и  соответственно:

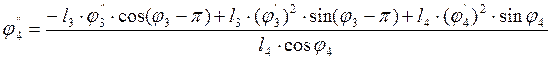  (3.31)

(3.32)

Дифференцируя по обобщенной координате уравнения (3.25) и (3.26), определяем аналоги ускорений центров масс звеньев 2 и 4 в проекциях на оси координат:

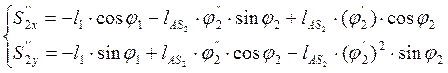  (3.33)

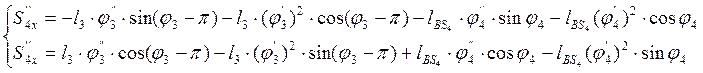(3.34)

По полученным формулам находим аналоги скоростей и ускорений интересующих точек и звеньев. Результаты расчетов на расчетное положение сводим в таблицы () и ().

3.6 Построение плана скоростей механизма.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем

Так как начальное звено совершает вращательное движение, то скорость точки A:

 

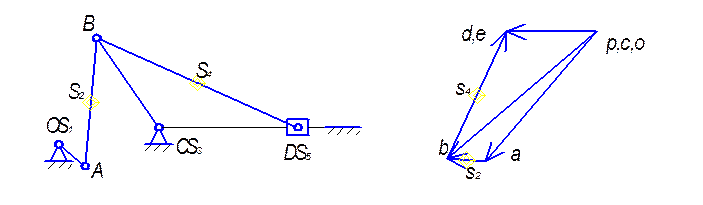Из полюса плана p – откладываем отрезок pa=50мм, изображающий вектор скорости A (Рис. 3.4).

 

Рис. 3.4 Построение плана скоростей

Подсчитаем масштабный коэффициент скоростей:

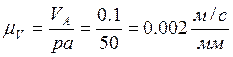
Для определения скорости точки B раскладываем плоскопараллельное движение звена 2 на переносное (поступательное) вместе сточкой A и относительное (вращательное) вокруг точки B. С другой стороны, точка B находится в относительном движении вокруг неподвижной точки C. Поэтому

  (3.35)

           

Уравнение (3.35) решаем графически. Через точку a проводим линию, перпендикулярную BA, а через полюс p – линию, перпендикулярную BC, до их пересечения в точке b. Векторы pb и  ab изображают искомые скорости  и .

Скорость точки D определяем аналогично, то есть раскладываем плоскопараллельное движение звена 4 на переносное (поступательное) вместе с точкой B и относительное (вращательное) вокруг точки B. С другой стороны, точка D находится в относительном движении относительно горизонтали x. Поэтому

  (3.36)

            

Уравнение (3.36) решаем графически. Через точку b проводим линию, перпендикулярную DB, а p – горизонталь, до пересечения в точке d. Векторы pd и bd изображают искомые скорости  и .

Положения точек и  на плане скоростей находим, воспользовавшись теоремой подобия:

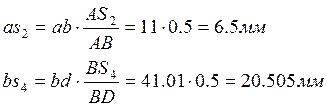
Векторы  и изображают скорости  и . Скорость точки  равна скорости точки D.

Из плана скоростей для расчетного положения находим

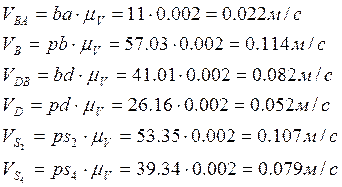
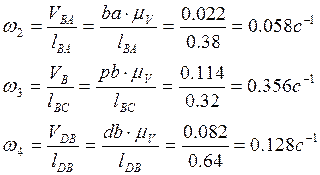
Определяем аналоги линейных и угловых скоростей:

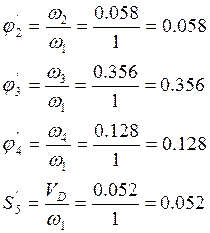
В табл. Приведены значения аналогов скоростей, полученные графическим и аналитическим методами.

Таблица 3.1

Результаты расчета аналогов скоростей.

Величина
Графически					-	-	-	-
Аналитически
D%					-	-	-	-

3.7 Построение плана аналогов ускорений кривошипно-ползунного механизма.

Задачу решаем путем построения плана ускорений, считая  постоянной величиной.

Определяем ускорение точки A. Полное ускорение точки A равно нормальной составляющей , которая направлена по линии OA к центру O:

 

Из полюса p откладываем вектор, изображающий ускорение точки A, в виде отрезка pa=50 мм (рис.).

Определяем масштабный коэффициент ускорений:

  

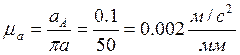
Для определения ускорения точки B записываем два векторных уравнения, рассматривая движение этой точки в начале со вторым звеном, а затем с третьим:

  (3.37)

           

 

          

 Нормальное ускорение определяем по формулам:

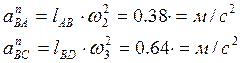
Отрезки, изображающие в миллиметрах векторы этих ускорений равны:

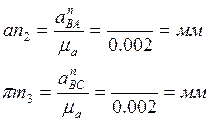
Вектор направлен вдоль линии BA от точки B к точке A – центру относительного вращения звена, а вектор  - по линии к центру C. Через точки и  плана ускорений проводим направления векторов касательных ускорений, пересечение которых определяет точку b – конец вектора искомого ускорения точки B.

Для определения ускорения точки D используем векторное уравнение:

  (3.38)

                 

Нормальное ускорение  определяем по формуле:

Отрезок, изображающий в миллиметрах вектор этого ускорения равен:

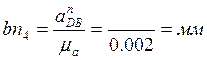
Вектор  направлен вдоль линии DB, от точки D к точке B – центру относительного вращения звена 4, а вектор – по горизонтали. Через точку  проводим вектор касательного ускорения, пересечение  и

определяет точку d – конец вектора искомого ускорения точки D.

Ускорения точек  и  находим, используя теорему подобия. Точки  и  делят отрезки ab и bd пополам. Ускорение точки  равно ускорению точки D.

Из плана ускорений находим:

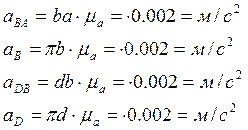
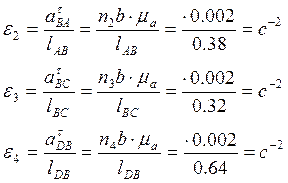
Направления угловых скоростей и ускорений звеньев для расчетного положения показан на плане положений механизма.

Учитывая, что, находим:

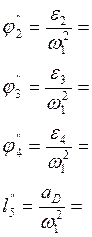
В таблицу сводим значения аналогов ускорений, полученных графическим и аналитическим методами для расчетного положения.

Таблица 3.2

Результаты расчета аналогов ускорений.

Величина
Графичеки					-	-	-	-
Аналттически
D%					-	-	-	-