Сравнение реакторов для некоторых частных случаев. Экспериментальное определение мгновенной селективности

8.3 Сравнение реакторов для некоторых частных случаев. 89

8.3.1 Две параллельные реакции произвольного порядка. 89

8.3.2 Три параллельные реакции. 90

8.4 Экспериментальное определение мгновенной селективности. 91

8.3 Сравнение реакторов для некоторых частных случаев

8.3.1 Две параллельные реакции произвольного порядка

Пусть имеют место две изотермические (т = const) реакции

ν₁₁А₁ → ν₂₁А₂,  (целевая реакция),

ν₁₂А₁ → ν₃₂А₃,  (побочная реакция).

Согласно (7.1), (5.1) баланс массы для трубчатого реактора

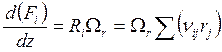,           (,), откуда для рассматриваемого случая

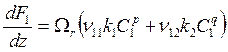;                                        (8.10)

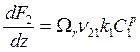.                                             (8.11)

Подставляя в (8.10) и (8.11) , на основании (2.16) получим

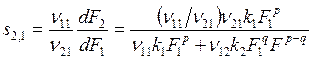.                                    (8.12)

С учетом того, что 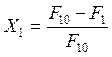 (см. (2.9)),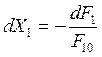

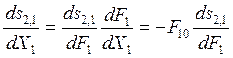.                                       (8.13)

Считая, что F (суммарный расход смеси) не зависит от конверсии, подставляя (8.12) в (8.13) и проводя дифференцирование, получим

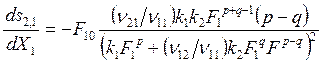.                                  (8.14)

Можно видеть, что знак производной  определяется только знаком разности (р - q).

Таким образом для рассматриваемого случая:

1) если q > р, то 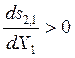 и, следовательно, интегральная селективность и выход в случае реактора идеального перемешивания выше;

2) если q < р, то 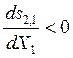 и, следовательно, селективность и выход выше в случае реактора идеального вытеснения;

3) если q = р, то 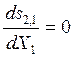, селективность и выход при заданной конверсии не зависят от типа реактора.

8.3.2 Три параллельные реакции

Пусть имеют место три изотермические (Т = const) реакции

ν₁₁А₁ → ν₂₁А₂,  (нулевой порядок),

ν₁₂А₁ → ν₃₂А₃,  (первый порядок, целевой продукт - А₃),

ν₁₃А₁ → ν₄₃А₄,  (второй порядок).

Уравнения баланса массы для А₁ и А₃ (см. (7.1), (5.1)):

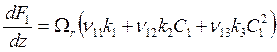;                                (8.15)

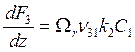.                                             (8.16)

Отсюда мгновенная селективность (см. вывод (8.12)

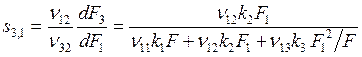.                           (8.17)

Аналогично (8.13) можно получить

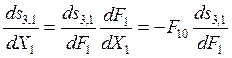,                                       (8.18)

откуда, после подстановки (8.17) в (8.16),

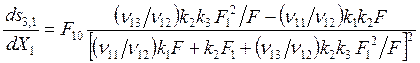.                  (8.19)

Знак производной  зависит от знака числителя правой части (8.19). Возможны следующие варианты:

1) , .

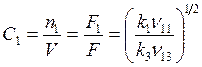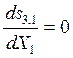Оба типа реакторов дают одинаковую селективность и выход.

2) , .

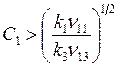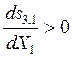Реактор идеального перемешивания обладает большими селективностью и выходом, чем реактор идеального вытеснения.

3) , .

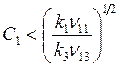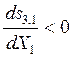Реактор идеального вытеснения обладает большим выходом, чем реактор идеального перемешивания.

В случае, если начальная концентрация С₁ удовлетворяет условию 1), а конечная концентрация – условию 3), то процесс целесообразно осуществлять с использованием двух последовательных реакторов: первый – реактор идеального перемешивания, второй – реактор идеального вытеснения.

8.4 Экспериментальное определение мгновенной селективности

Зависимость селективности от конверсии проще всего определять экспериментально с использованием реактора идеального перемешивания, так как для реактора идеального перемешивания (см. (8.7)) . В этом случае по измеренным концентрациям реагентов и продуктов на выходе из реактора рассчитываются величины  и X_i и строится зависимость .

В случае трубчатого реактора идеального вытеснения связь между мгновенной селективностью, конверсией и суммарной селективностью более сложная.

Пусть идеальная реакция представляется уравнением

ν₁₁А₁ → ν₂₁А₂                                                         (8.20)

Мгновенная селективность (см. (2.16))

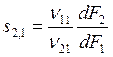.                                                 (8.21)

Суммарная селективность (см. (2.15))

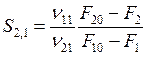,                                           (8.22)

откуда

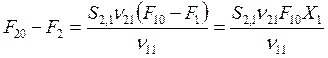;                       (8.23)

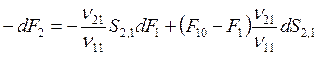.                         (8.24)

Далее, подставляя (8.24) в (8.21), получим

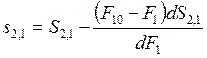.                                 (8.25)

Учитывая, что в соответствии с (2.9)

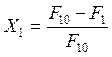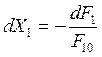, ,                              (8.26)

из (8.25) можно получить

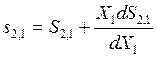                                           (8.27)

или

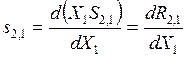.                                     (8.28)

Таким образом, для того чтобы определить мгновенную селективность на основе экспериментальных данных, полученных на трубчатом реакторе идеального вытеснения, необходимо определить зависимость суммарной селективности от степени превращения на выходе реактора, определить по этой зависимости производную  и рассчитать  на основании зависимости (8.27). Соотношение (8.28) дает мгновенную селективность как производную выхода по степени превращения.