Влияние свойств теплоотдающей стенки на теплообмен при кипении, страница 2

                                        (4)

В [2] показано, что динамический угол смачивания  один из наименее исследованных параметров роста паровых пузырей на твердой поверхности. Зависимости для его вычисления отсутствуют. Число действующих центров парообразования в [2] рекомендуется определять по формуле                                                                (5)

Здесь     и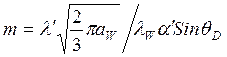    

Число центров парообразования трудно вычислить при отсутствии экспериментальных данных. В выражении (5) коэффициент пропорциональности не является константой, а может изменяться в несколько раз в зависимости от сочетания металла теплоотдающей стенки и кипящей на ней жидкости [2].

Входящая в (4) величина  может быть рассчитана по формуле

                                                              (6)

Коэффициент пропорциональности b в зависимости Лабунцова (6) может быть определен только после обработки экспериментальных данных.

Если воспользоваться результатами опытов, опубликованных в [25], то можно при некоторых предположениях оценить значения  при кипении фреонов. Особенностью опытов, представленных в [25], является широкое изменение температуры насыщения (от -40°С) до +40°С) при малом значении удельного теплового потока. Опыты сопровождались скоростной киносъемкой, результаты обработки которой представлены в табличном виде.

Кроме и  указаны среднестатистические значения радиуса пузыря и время его роста при данном давлении. Определенные экспериментально время роста пузыря и его радиус позволяют вычислить коэффициент пропорциональности в зависимости Лабунцова (6)

                                                                          (7)

По данным Даниловой [25] при кипении фреонов среднее значение . Обобщение большого числа экспериментальных данных по отрывному диаметру пузыря, опубликованное в [26], позволяет определить радиус пузыря для любых давлений. Аппроксимационная зависимость, приведенная в [26], имеет вид

                                                  (8)

где

Если предполагать, что динамический краевой угол смачивания  при кипении фреонов и азота одинаков, то, используя зависимости (5), (7), можно приближенно вычислить значение  по (4). Такое предположение возможно вследствие того, что фреоны так же хорошо смачивают поверхности металлов, как криогенные жидкости. При выполнении оценочных расчетов по определению глубины захолаживания  значения  считались не зависящими от температуры насыщения и для всех фреонов принимались одинаковыми. Угол между образующей конической поверхностью микрослоя и поверхностью нагрева (см. рис. 1) оценивался по [27], где приведена формула для вычисления толщины пленки под растущим пузырем. Значение коэффициента пропорциональности  в формуле (5) принималось равным .

С учетом принятых предположений вычисление глубины захолаживания можно рассматривать как параметр, определенный по порядку величины. Поэтому только при условии  теплоотдающая стенка рассматривалась как "толстостенная" (см. табл. 1). Точки, представленные на рис. 2 и последующих рисунках, соответствуют этому условию.

Опыты при кипении других жидкостей [33, 34, 35], которые включены в таблицу 1, выполнены при охлаждении торца теплоизолированного стержня, поэтому можно без оценок такой участок считать «толстостенным».

На рис. 3 показаны результаты обработки экспериментальных данных, приведенных в табл. 1, по теплообмену при кипении фреонов на толстостенных трубах из различных материалов. Они сопоставлены с опубликованными в монографии Григорьева и др. [2] данными подобных опытов при кипении азота. Сравнение выполнено в координатах

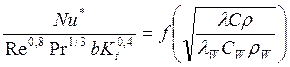                                    (9)

Из рис. 3 видно, что теплообмен при кипении фреонов, так же как и при кипении азота, является функцией комплексного критерия .

Сравнение опытов в координатах (9) предполагает, что опыты всех  авторов, чьи данные показаны на рис. 3, выполнены на толстостенных нагревателях, имеющих одинаковую относительную шероховатость. В действительности последнее условие строго не выполнялось, что и привело к дополнительному разбросу данных, при сравнении опытов даже при кипении фреонов.