Сравнение точности нахождения результата алгоритмом отжига и аналитическим методом

ИТ-031

Голомаздин С.М.

Лабораторная работа №1

3. Количество городов равно 10. Сравнить точность нахождения результата алгоритмом отжига и аналитическим методом. Функция охлаждения 2.3.

2.3.     T[i] = To*(Tn/To)^(i/N)

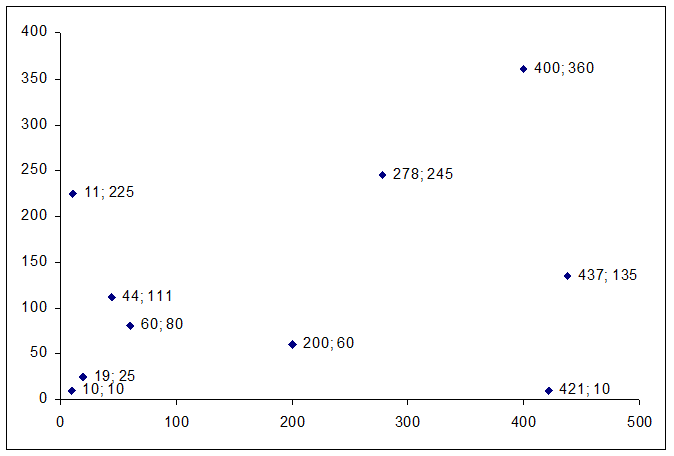
Длина пройденного пути равна 1213,02

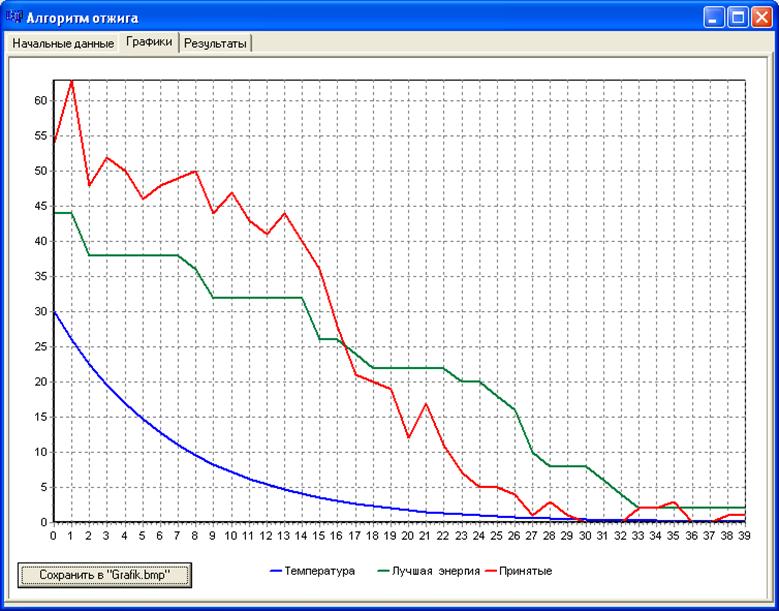
3. Сравнить функции 2.3 и 2.9.  Начальные параметры: количество ферзей 50; Количество итераций при одной температуре 150-200; Конечная температура 0.1-0.5;

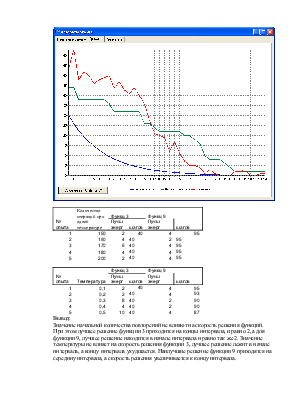
Вывод:

Значение начальной количества повторений не влияют на скорость решения функций. При этом лучшее решение функции 3 приходится на концы интервала, и равно 2, а для функции 9, лучшее решение находится в начале интервала и равно так же 2. Значение температуры не влияет на скорость решения функции 3, лучшее решение лежит в начале интервала, а концу интервала ухудшается. Наилучшие решение функции 9 приходятся на середину интервала, а скорость решения увеличивается к концу интервала.