Голомаздин С.М.
Лабораторная работа №4
Исследование влияния начальных параметров генетических алгоритмов на скорость и точность нахождения оптимального решения задачи коммивояжера
Цель работы: обретение навыков оптимальной настройки параметров генетических алгоритмов при решении задачи коммивояжёра; сравнение точности нахождения результата ГА с аналитическими методами решения.
Задание: Исследовать влияние количества поколений и вероятности мутации на скорость нахождения результата и его точность при количестве городов равным 30. Города расположить по кругу. Размер поля принять равным 1000х1000. Сравнить точность нахождения результата генетическими алгоритмами и методом кратчайшего незамкнутого пути.
Код программы
Public Class Form1
Const PI = 3.14, N = 30, R = 500 ' N-Количество городов, R-радиус круга
Dim PopSize As Integer ' Размер популяции
Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click
График зависимости длины усреднённого пути всех хромосом от поколения.
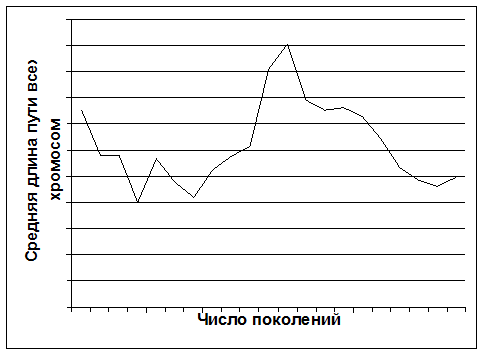
Усредненный путь всех хромосом имеет тенденцию к уменьшению с увеличением числа поколения. Однако наблюдаются и увеличения пути ввиду наличия вероятности мутации.
График зависимости длины лучшего пути от поколения.
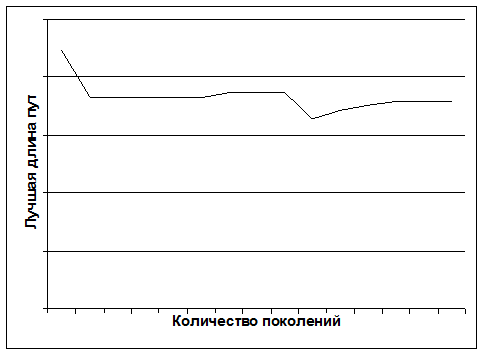
Длина лучшего пути с увеличением числа поколений имеет тенденцию к уменьшению, что объясняется «естественным отбором», т.е. из поколения в поколение отбираются лучшие экземпляры и в результате появляются потомки со все более лучшим набором ген.
График зависимости числа шагов (обратно пропорционален скорости) от размера популяции.
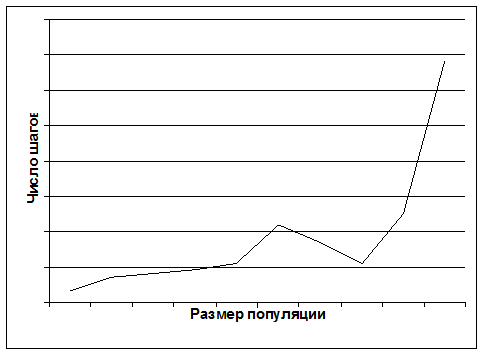
С увеличением размера популяции увеличивается число шагов для нахождения лучшего решения, т.е. уменьшается скорость. Это объясняется тем, что при большем размере популяции «схождение» хромосом происходит дольше.
График зависимости длины пути от размера популяции.
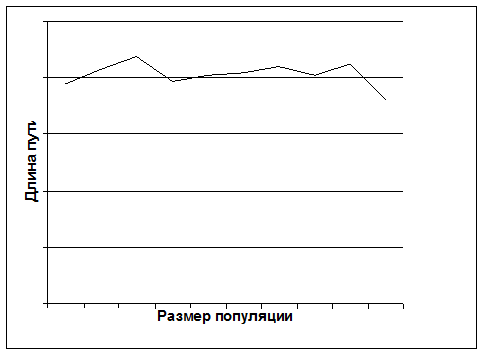
С увеличением размера популяции длина имеет тенденцию к незначительному уменьшению.
Сравнить точность нахождения результата генетическими алгоритмами и методом кратчайшего незамкнутого пути.
Кратчайший незамкнутый путь для городов расположенных по кругу – это последовательный их перебор. Для нахождения длины пути достаточно найти путь между двумя соседними городами и умножить на количество городов.
Длина пути между двумя соседними городами:
X=2R*sin(360/N/2), где R-радиус круга, N-число городов
Длина кратчайшего незамкнутого пути:
L=N*X=2NR*sin(360/N/2)=3135
Решение найденное программой – 3256,1285, т.е. ошибка составляет около 3.8%.
Сравнить скорость нахождения результата генетическими алгоритмами и способом полного перебора. Взять время одного перебора равным 0,0001 секунды.
Число городов N=30, тогда общее число возможных вариантов N!, время необходимое для полного перебора T=0,0001*N!= 7368134994783084962119680 часов.
Скорость же нахождения решения генетическим алгоритмом составила в среднем от 2 до 10 сек.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.