(а) Тенденцию к агломерации во влажной атмосфере;
(б) Тенденция к агломерации при температуре, близкой к точке плавления.
При анализе возможности псевдоожижения необходимо определить три гидродинамические величины:
(а) Минимальную скорость псевдоожижения ![]() .
.
(б) Скорость уноса, по крайней мере, части твердых частиц.
(в) Степень расширения слоя как функцию ![]() .
.
Два существенных замечания:
1. При разработке аппаратов с псевдоожиженным слоем необходимо, исходя из требования оптимального использования объема, подбирать условия минимального расширения слоя и одновременно гарантирующих хорошую подвижность частиц и хорошее перемешивание. Это обычно достигается при расширении порядка 10-20%. Применение скоростей псевдоожижения, приводящих к значительным расширениям обычно неприемлемо. Но иногда это может иметь место, чтобы обеспечить гибкость в эксплуатации. Если возможно существенное увеличение скорости псевдоожижения, вопрос о расширении слоя должен быть тщательно изучен.
2. В случае классического псевдоожижения твердые частицы остаются в слое все время. Некоторый унос предотвращается за счет использования циклонов и/или других систем, предотвращающих захват частиц потоком. Фактически, в последнее время, особенно при разработке процессов каталитического крекинга, реакционная зона была сдвинута из собственно псевдоожиженного слоя в линию транспорта частиц. В этом случае реактор крекинга превратился в трубу, в которой реактанты и катализатор движутся в спутном потоке. В этом случае уже можно говорить не о псевдоожиженном слое, а о циркулирующем слое. Циркулирующий слой интенсивно изучается в настоящее время применительно к газификации и сжиганию угля.
2.3.3. Минимальная скорость псевдоожижения ![]()
Рассмотрим наиболее простое приближение, позволяющее
понять физический смысл скорости минимального псевдоожижения. Если измерять
перепад давления на слое, одновременно увеличивая скорость газа, то можно
получить зависимость, подобную показанной на Рис. 2.16. Пока скорость газа, то
можно получить зависимость, подобную показанной на Рис. 2.16. Пока скорость
газа не достигнет ![]() перепад давления будет
возрастать при увеличении скорости, аналогично тому, как это имеет место в
неподвижном слое. На этом участке изменение
перепад давления будет
возрастать при увеличении скорости, аналогично тому, как это имеет место в
неподвижном слое. На этом участке изменение ![]() зависимость
перепада давления от скорости может быть рассчитана на основе уравнения Эргана:
зависимость
перепада давления от скорости может быть рассчитана на основе уравнения Эргана:
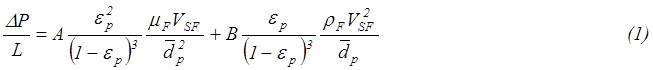
где
![]() - доля слоя, занятая частицами.
- доля слоя, занятая частицами.
Рис. 2.16 Общий перепад давления в слое как функция скорости псевдоожижения. Прерывистая линия соответствует первому циклу псевдоожижения
(сначала порозность слоя наименьшая)
Очевидно, что силы трения, действующие на слой
вызывают падение давления, возрастающее с увеличением скорости газа. Момент
выхода на постоянное значение ![]() соответствует равенству
веса слоя и сил трения, действующих на слой. Затем давление остается постоянным
благодаря тому, что при дальнейшем увеличении скорости частицы приобретают
подвижность и порозность слоя увеличивается с увеличением скорости газа.
Постепенно расстояние между частицами становится таким, что каждую частицу
можно рассматривать как одиночную. В этот момент взаимодействие частицы с
потоком аналогично тому, которое имеет место при свободном осаждении частиц.
Скорость газа, при которой это условие выполняется, называется скоростью уноса
соответствует равенству
веса слоя и сил трения, действующих на слой. Затем давление остается постоянным
благодаря тому, что при дальнейшем увеличении скорости частицы приобретают
подвижность и порозность слоя увеличивается с увеличением скорости газа.
Постепенно расстояние между частицами становится таким, что каждую частицу
можно рассматривать как одиночную. В этот момент взаимодействие частицы с
потоком аналогично тому, которое имеет место при свободном осаждении частиц.
Скорость газа, при которой это условие выполняется, называется скоростью уноса ![]() . Диапазон скоростей от
. Диапазон скоростей от ![]() до
до ![]() является
диапазоном псевдоожижения. Перепад давления на слое в этом диапазоне остается
независимым от скорости газа. Таким образом, скорость минимального
псевдоожижения можно определить из баланса силы сопротивления, определяемого
уравнением Эргана для неподвижного слоя и силы всего слоя:
является
диапазоном псевдоожижения. Перепад давления на слое в этом диапазоне остается
независимым от скорости газа. Таким образом, скорость минимального
псевдоожижения можно определить из баланса силы сопротивления, определяемого
уравнением Эргана для неподвижного слоя и силы всего слоя:
![]()
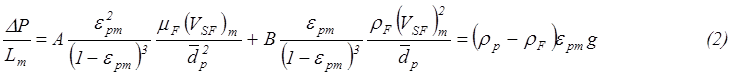
где
![]() - доля частиц в слое на
границе перехода к состоянию псевдоожижения
- доля частиц в слое на
границе перехода к состоянию псевдоожижения
![]() - плотность частиц
- плотность частиц
Чтобы перейти к безразмерному виду умножим правую и левую части на выражение:
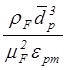
При этом можно получить:
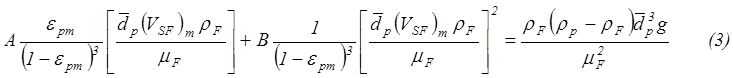
где
 - число Рейнольдса
- число Рейнольдса ![]() ,
,
 - число Архимеда
- число Архимеда ![]() .
.
Поэтому (3) можно переписать в виде:
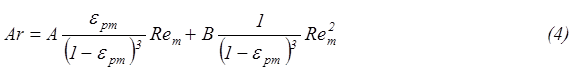
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.