Реактор с неподвижным слоем катализатора и одной текучей фазой, страница 4

§  Если в случае газовой фазы при высоте слоя Н>100необходимо достигнуть конверсии главного реактанта Х₁>0,9, то массообмен не должен лимитировать скорость процесса. Фактически, если реакция очень быстрая внутри зерна, то процесс полностью контролируется внешней диффузией, и конверсия определяется соотношением (2.24):

Ранее было показано, что:

а 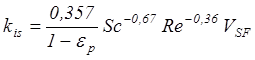           (экспериментальные данные, 3<Re<2000)               (2.24)

откуда

Зная, что для газов , а , для конверсии 90% (т.е. для 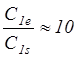) можно записать:

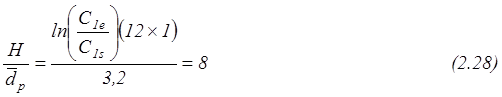
В действительности, для гарантии, эта величина должна быть еще больше. Поэтому практическое правило Саттерфилда устанавливает: .

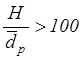Если текучая среда – жидкость, ситуация меняется. Для этих условий . При этом, для того, чтобы получить 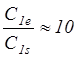, необходимы очень большие значения  - порядка 10⁴. Это говорит о том, что в случае, когда текучая среда – жидкость, очень трудно избавиться от влияния внешней диффузии.

2.1.7. Теплообмен на стенке реактора

Адиабатический реактор обычно более предпочтительный, т.к. им проще управлять.

В некоторых случаях экзо- (эндо-) термических реакций, адиабатический реактор в принципе невозможен. В этих случаях необходимо подводить (или отводить) тепло из (к) зоны катализа.

Для неподвижного слоя отвод тепла сопровождается появлением температурного градиента в слое. Этот градиент, подобно осевому температурному градиенту, может быть описан на основе введения слагаемого, отражающего диффузию тепла, подобно тому, как это делалось в случае концентрационного градиента.

Из уравнения баланса энтальпии можно получить, что определяющими параметрами являются:

(а) Осевое число Пекле, содержащее осевую эффективную теплопроводность.

(б) Радиальное число Пекле, содержащее радиальную эффективную теплопроводность.

(в) Новый параметр: коэффициент теплоотдачи на стенке.

Проблема теплообмена со стенкой теплообменника достаточно сложная, поэтому будем использовать упрощенную пленочную модель, которая часто применяется при рассмотрении гранулы.

При этом реальный градиент температур вблизи стенки заменим на линейный в соответствии с рис. 2.4, где:

 - средняя температура в жидкости,

 - температура жидкости на стенке со стороны слоя.

 

Рис. 2.4. Пленочная теория применительно к теплопереносу от стенки к слою гранул

В данном представлении баланс энтальпии для цилиндрического слоя толщиной dz в упрощенном виде имеет вид:

 

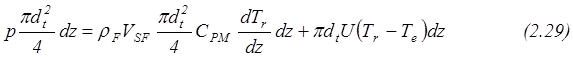
где

- объемный источник тепла при средней температуре  и средней концентрации в сечении z (расстояние от входа реактора) (Вт/м³)

 - диаметр реактора (м)

 - плотность жидкости  (кг/м³)

 - средняя по сечению скорость жидкости при   (м³/м²×с)

 - теплоемкость жидкости при  (Дж/(кг×К))

 - средняя температура газа (флуида) (К)

 - температура охлаждающей жидкости

U – коэффициент теплопередачи через стенку (Вт/(м²×К))

: массовый расход жидкости через единицу площади сечения (кг/(м²×с)) (не зависит от температуры и давления).

Выражение (2.29) можно переписать в виде:

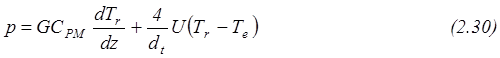
Это соотношение соответствует случаю, когда температуры газа и гранул равны, хотя иногда, как это было сказано выше, это может быть и не так.

Коэффициент теплопередачи определяется выражением:

где

 - коэффициент теплоотдачи со стороны слоя (Вт/(м²К)),

 - коэффициент теплоотдачи со стороны охлаждающей (нагревающей) жидкости (Вт/(м²К)),

 - толщина стенки, (м)

 - теплопроводность материала стенки (Вт/(м×К)),

 - поверхность теплообмена, контактирующая со слоем (м²),

 - поверхность теплообмена, контактирующая с охлаждающей жидкостью (м²),

 - среднее логарифмическое между  и  (м²).

Если стенка достаточно тонкая или достаточно высокая теплопроводность  , то (2.31) можно переписать в виде:

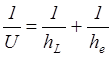
 - дается в соответствующей литературе по теплопереносу в зернистых слоях.

Например,

§  Для случая нагрева слоя

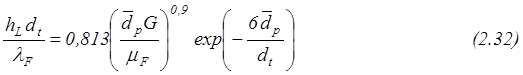
§  Для случая охлаждения слоя

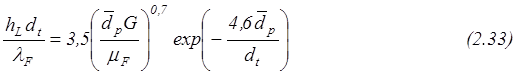
где

 - теплопроводность фильтрующегося агента,