Промышленность \ Расчет и конструкции химических реакторов

Реактор с неподвижным слоем катализатора и одной текучей фазой, страница 3

Эффект аксиальной дисперсии может быть определен на основе перехода от фактора эффективности e к eD. При этом конверсия опишется уравнением:

,           где

С другой стороны, без введения eD, при наличии осевой диффузии, можно получить:

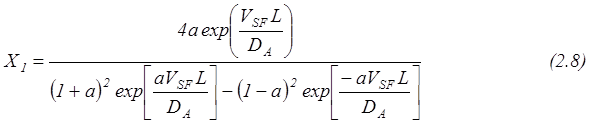
где

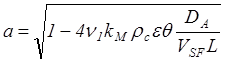
Разлагая в ряд экспоненциальные и квадратичные выражения, можно получить:

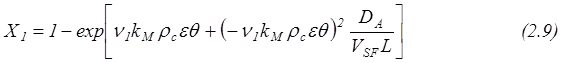
Сопоставляя (2.2b) и (2.9.) можно получить связь eD и e для (2.2b) относительно низких величин DA/(VSFL):

которое, с учетом того, что q=V/Q и VSF=Q/S можно переписать в виде:

Необходимо обратить внимание на примененный путем формального перевода уравнения одного вида (2.8.) в уравнение другого вида (2.2b) с получением соотношения, связывающего соответствующие эффективные параметры, отражающие различные физические условия процесса.

2.1.4.2. Графическое вычисление конверсии X1

Для вычисления (численного или графического) конверсии вещества А1 в случае реакции 1-го порядка в изотермических и изобарических условиях, необходимо рассмотреть 5 уравнений:

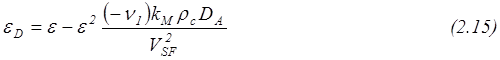
Графическое решение можно получить используя рис. 2.2, оперируя безразмерными параметрами:

где

Порядок действий

Сначала вычисляется модуль Тиле Ф. Используя нижний правый квадрант, можно получить h. Затем, проецируя на кривые верхнего правого квадранта, определяем e для соответствующего значения  .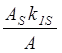

Проецируя на верхний левый квадрант, на кривую, соответствующую величине, получаем eD. Нижний левый квадрант дает конверсию для соответствующей величины.  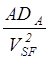можно представить в виде:

где  - обратная величина числа Пекле.

2.1.5. Расчет падения давления в реакторе с неподвижным слоем

Падение давления на высоте неподвижного слоя можно определить на основе уравнения Эргана.

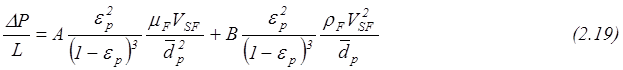
где

eр=1-e, e - порозность слоя

Для однородных слоев, состоящих из сферических частиц одного и того же размера коэффициенты А и В имеют следующие значения:

А=150,

В=1.75.

Чтобы адаптировать уравнение Эргана на случай, когда слой содержит частицы разного размера или несферические частицы необходимо коэффициенты А и В или даже групповые параметры:

              и                

Определять на основе лабораторных измерений перепадов давлений в трубе при условии, что 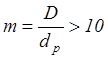 (обычно в качестве газа используют воздух).

Уравнение Эргана остается пригодным для жидкостей (газов) с различными свойствами. Те не менее, всегда необходимо очень точно знать величину eр, так как DР очень сильно зависит от этого параметра.

Если такие лабораторные измерения невозможны, всегда можно сделать оценки, основанные на следующих экспериментальных данных:

(а) Порозность (1-eр) нормально упакованного слоя обычно составляет 0,38±0,42

(б) В то же время для слоя катализатора часто (1-eр)»0,42

После некоторого времени эксплуатации eр®0,38 (часто это max eр). Способ загрузки может влиять на eр.

 в уравнении Эргана можно вычислять по формуле:

 

Но могут применяться и другие формулы. Разные формулы обычно совпадают, если распределение частиц по размерам относительно узкое.

2.1.6. Влияние внешнего массопереноса в реакторе с неподвижным слоем

Профили температуры и концентрации показаны на рис.2.3.

Зная коэффициенты внешнего тепло- и массопереноса  и , соответственно, можно получить распределения температуры и концентраций в виде (2.22) и (2.23).


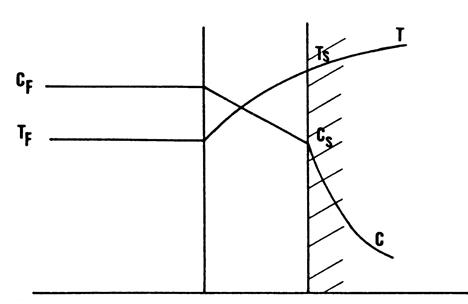Рис. 2.3. Температурный и концентрационный профили в жидкой фазе, пленке и грануле.

Экзотермическая реакция.

Формулы для hFS и kiS можно найти в справочниках разные в зависимости от диапазона числа Re, соответствующего рассматриваемым условиям, в виде .

Для газовой фазы можно получить, что максимальный перепад температур между гранулой и потоком составляет:

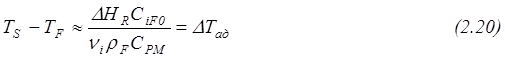
Критерий оценки влияния внешнего массопереноса

Возможное влияние массопереноса может быть оценено на основе простого правила Сэттерфилда:

Скачать файл