Анализ и синтез линейной непрерывной системы автоматического управления

Построение асимптотической ЛАЧХ нескорректированной системы -  в разомкнутом состоянии.

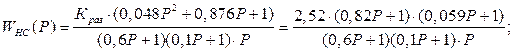
При построении ЛАЧХ системы, состоящей из последовательных типовых звеньев учитывается, что логарифм произведения есть сумма логарифмов, поэтому для каждого звена можно построить ЛАЧХ, а затем просуммировать и получить ЛАЧХ всей системы.

Для построения  рассчитываем необходимые параметры:

1). дБ;

2). частоты сопряжения системы:

рад/с, форсируещее звено;

рад/с, апериодическое звено;

рад/с, апериодическое звено;

рад/с, апериодическое звено;

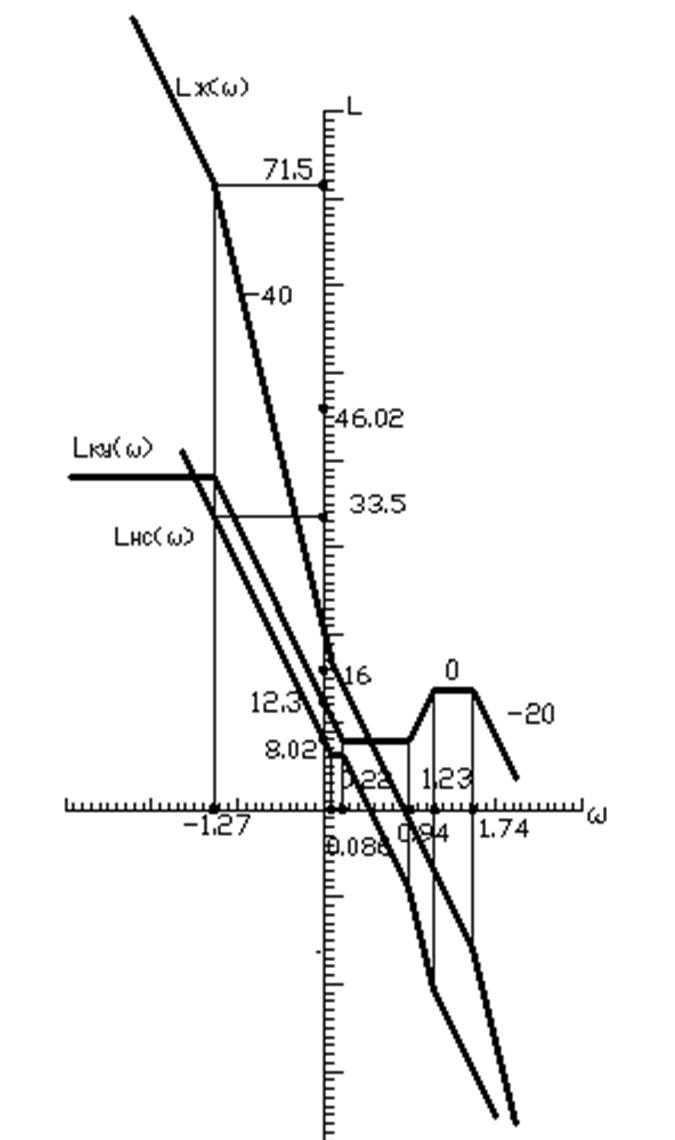
Построение нескорректированной ЛАЧХ.

В координатной плоскости [L(w), w] при частоте w=1(lg1 = 0 дек) отложим ординату , а также частоты сопряжения.

Построение ведем слева направо. В низкочастотной области (до минимальной частоты сопряжения) асимптотическая - прямая линия, проходящая под наклоном -20 дБ/дек, через точку с координатами ( , 0). При частотах сопряжения апериодических звеньев наклон изменяется на    -20 дБ/дек, форсирующих +20 дБ/дек. Таким образом, асимптотическая представляет собой ломаную с наклонами

-20, 0, -20, -40 и -20 дБ/дек.

Построение асимптотической желаемой ЛАЧХ -.

Желаемая ЛАЧХ астатической скорректированной САУ  должна обеспечивать заданные показатели качества переходных процессов , .

Построение низкочастотной зоны . По номограммам, задавшись требуемыми значениями перерегулирования и временем регулирования, определим максимальное значение вещественной частотной характеристики  и найдем частоту среза:

;

;

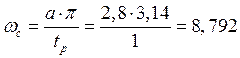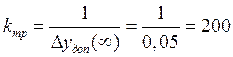
Определим ординаты начала и конца среднечастотной зоны.

Ординаты начала и конца СЧЗ ориентировочно берутся равными требуемому запасу устойчивости по модулю  с разными знаками. Требуемые запасы устойчивости по модулю и по фазе можно найти по номограмме.

При  требуемый запас устойчивости по модулю дБ, по фазе .

Среднечастотная асимптота  проводится под наклоном -20 дБ/дек через точку на оси абсцисс, имеющую частоту в логарифмическом масштабе  . Начальную и конечную ординаты принимаем ±16 дБ.

Высокочастотная зона  в целях простоты реализации корректирующего устройства (регулятора) строится параллельно ЛАЧХ исходной САУ, причем ее наклон должен составлять -40 дБ/дек.

Среднечастотную и низкочастотную зону  сопрягаем линией под наклоном -40 дБ/дек. Этой графической операцией завершается построение асимптотической желаемой ЛАЧХ.

Восстановим передаточную функцию с учетом численных значений.

Передаточная функция состоит из (смотрим слева направо):

1). Интегрирующее звено: ;

2) Апериодическое звено: ;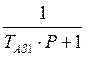

3). Форсирующее звено: ;

4). Апериодическое звено: .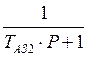

Передаточная функция “желаемого устройства” примет вид:

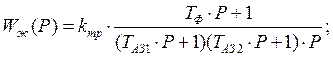
вычислим значения Т:

ЛАЧХ последовательного корректирующего устройства.

Построим ЛАЧХ  последовательного корректирующего устройства графическим вычитанием ординат из ординат .

Восстановим передаточную функцию с учетом численных значений.

Передаточная функция состоит из:

1) Апериодического. звена: ;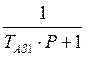

2). Форсирующего звена: ;

3). Форсирующего звена: ;

4) Апериодического. звена: ;.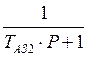

5). Апериодического звена: ;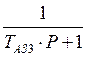

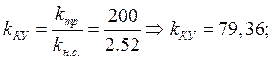
Передаточная функция корректирующего устройства примет вид:

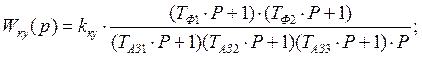
вычислим значения Т:

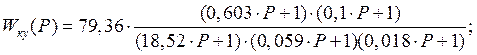
Определяем показатели качества переходных процессов, выполнив моделирование на ПК в программе Mathlab. Для моделирования используется  структурная схема с корректирующим устройсвом, в которой все элементы представлены в виде типовых звеньев, содержащихся в библиотеке программы.

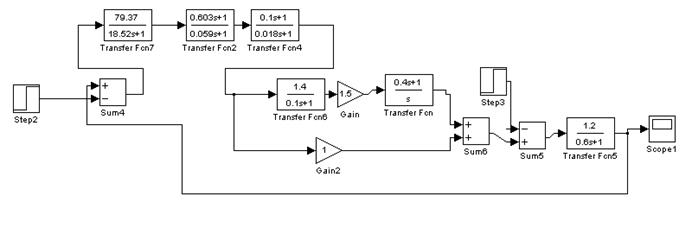Переходные процессы получаем как реакцию системы на единичные ступенчатые задающие и возмущающие воздействия.

На рисунках представлены графики переходного процесса при подаче постоянного сигнала по управлению и возмущению.

Реакция скорректированной САУ по задающему воздействию:

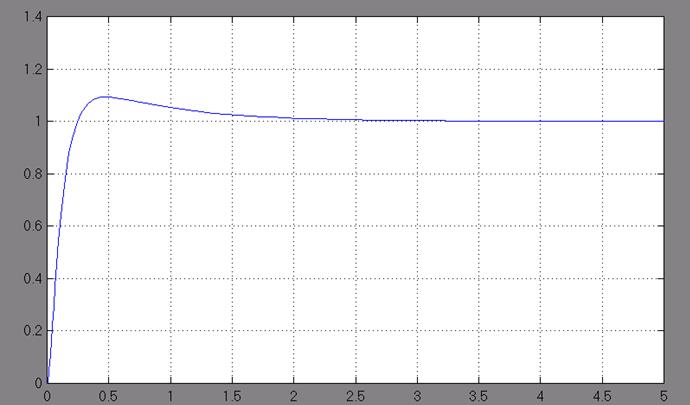Время переходного процесса t=1(с)

Перерегулирование σ=10%

Реакция скорректированной САУ по возмущающему воздействию:

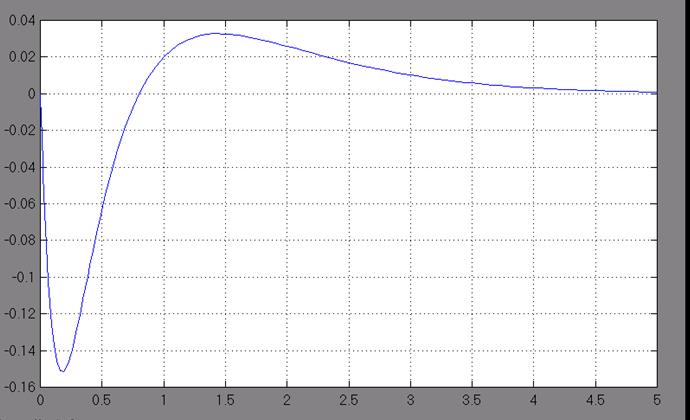
Время переходного процесса t=1(с)

Вывод.

В результате проведенной коррекции быстродействие системы уменьшилось.

Кроме того, скорректированная система отвечает требованиям: