uj - Dj/2 £ uАИМ(iTд)
£ uj
+ Dj/2, (1.5)
|
|
то
квантованному импульсу
uкв(iTд) присваивается амплитуда разрешенного
uj уровня квантования. При этом возникает ошибка
квантования d
кв, представляющая
разность между передаваемой квантованной величиной и истинным значением
непрерывного сигнала в данный момент времени
dкв (iTд)
= uкв(iTд)
– uАИМ(iTд). (1.6)
|
|
Как следует из рисунка 1.3, ошибка квантования лежит в пределах
Амплитудная характеристика квантующего устройства
приведена на рисунке 1.4.

Если ошибки квантования распределены по случайному
закону и не коррелированны друг с другом, то совокупный эффект от них в системе
с ИКМ можно рассматривать как аддитивные шумы, имеющие субъективное воздействие,
которое аналогично воздействию белого шума с ограниченной полосой [1].
Определим мощность шумов квантования, для чего разобьем
весь диапазон изменения мгновенных значений аналогового сигнала от –uогр до uогр на N шагов
квантования (рисунок 1.5) [2].
Один из шагов квантования uj
от uj-Dj/2 до uj+Dj/2 отмечен на
оси абсцисс; непрерывный сигнал, попадающий в пределы этого шага, обозначим uj`.
Вероятность появления сигнала с уровнем, лежащим в пределах j-го
шага квантования
|
|
Pj (uj-Dj/2 £ u £ uj+Dj/2 ) = 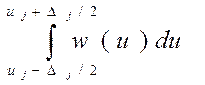 (1.8) (1.8)
|
|
Эта вероятность определяется площадью заштрихованного
участка под кривой w(u) на рисунке 1.5. Поскольку шаг квантования мал по
сравнению с диапазоном изменения напряжения непрерывного сигнала, то из (1.8)
получим
|
|
Pj (uj-Dj/2 £ u £ uj+Dj/2 ) » w(uj)´Dj , (1.9)
|
|
где w(uj`) – плотность вероятности напряжения непрерывного
сигнала, попадающего в рассматриваемый интервал. Мгновенная мощность шума квантования,
развиваемая на сопротивлении 1 Ом
Мощность шума квантования, возникающего при квантовании
напряжения сигнала, лежащего в пределах j-го шага квантования
|
|
Pквj =  (1.10) (1.10)
|
|
Pквj = 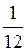 ´D2j´ pj . (1.11) ´D2j´ pj . (1.11)
|
|
C учетом (1.8, 1.9) из (1.10) получим
Полная мощность шумов квантования на сопротивлении 1 Ом
равна сумме составляющих шумов от каждого шага квантования (1.11)
Ркв =
 ´ D2j ´ pj
. (1.12) ´ D2j ´ pj
. (1.12)
|
|
Поскольку практически все дискретные значения
непрерывного сигнала находятся в пределах зоны квантования от –uогр до uогр
(рисунок 1.6), то
|
|
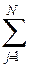 pj
= 1, и при Dj = D0 Pкв= pj
= 1, и при Dj = D0 Pкв=
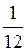 D02
. (1.13) D02
. (1.13)
|
|
Из выражения (1.13) следует, что при равномерной шкале
квантования мощность шума квантования не зависит от уровня квантуемого сигнала
и определяется только величиной шага квантования. При этом отношение сигнал/шум
квантования
|
|
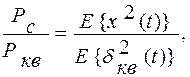 (1.14)
(1.14) (1.14)
(1.14)
|
|
где Е {x2(t)}, E{dкв2 (t)} –
математическое ожидание или среднее значение аналогового сигнала и ошибки
квантования, соответственно. С учетом (1.13) из (1.14) получим
|
|
Рс /Ркв
= 10 lg [x2 / (D2/12)] = 10,8 + 20lg(n/D), (1.15)
|
|
где n – среднее квадратическое
значение амплитуды сигнала. В частности, для синусоидального входного сигнала
отношение сигнал/шум квантования при равномерном квантовании
|
|
Рс/Ркв = 10lg[(A2/2)/(D2/12)]=7,78 + 20lg(A/D), (1.16)
|
|
где А – амплитуда
синусоиды.

