Преобразование аналоговых сигналов в цифровую форму

1.5.1. Пояснить процесс преобразования непрерывного сигнала в импульсно-кодовомодулированный : дискретизация , квантование , кодирование .

Цифровые системы передачи . Носов. Эл. Учебник.

1.2 Преобразование аналоговых сигналов в цифровую форму

1.2.1 Дискретизация непрерывного сигнала

Первым шагом в преобразовании аналогового сигнала u_k(t) в цифровой является формирование последовательности дискретных моментов времени r(t), в которые осуществляется дискретизация сигнала. Если дискреты формируются достаточно часто, то исходный сигнал может быть полностью восстановлен из последовательности дискретов путем применения фильтра нижних частот для интерполяции или формирования сглаженного по величинам дискретов сигнала. Эти основные понятия иллюстрирует рисунок 1.1.

Классические результаты в системах с дискретизацией были получены В.А. Котельниковым (1931 г.) и Г. Найквистом (1933 г.), которые определили минимальное значение частоты дискретизации, необходимое для извлечения всей информации из непрерывного, меняющегося во времени сигнала. Согласно теореме В.А. Котельникова частота дискретизации F_Д непрерывного, ограниченного по спектру сигнала, с верхней частотой F_В много больше F_Н, должна быть

	FД> 2 FВ ,        ТД > 1 / FД               (1.1)

 

При АИМ (рис. 1.1) в соответствии со значениями непрерывного со-общения u_k(t), изменяется амплитуда импульсов r(t) на выходе модулятора. Последовательность немодулированных импульсов r(t) длительностью t_и и периодом повторения  Т_Д может быть записана

r(t) = 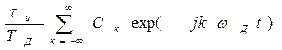,    (1.2)

где С_к=sin(pkt_и/Т_Д)/ (pkt_и/Т_Д); С₀=1; w_Д=2pF_Д.

 

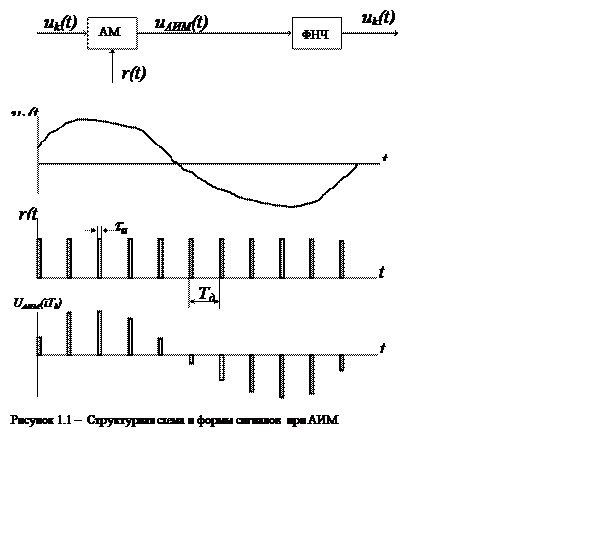Сигнал на выходе модулятора может быть определен как произведение двух входных сигналов

	uАИМ(t) = uk(t) ´ r(t).                    (1.3)

 

SАИМ(w) =(1.4)

                                                                                                                  

Если известен спектр непрерывного сообщения S_u(w) и из (1.2) определен спектр импульсной последовательности S_r(w), то из (1.3) можно определить спектр АИМ сигнала

При k = 0 из (1.4) следует

	SАИМ(w) = (tи/ТД)2 ´ Su(w),

 

Таким образом, спектр АИМ сигнала можно получить, если учесть, что непрерывная последовательность импульсов r(t) имеет частотный спектр, состоящий из дискретных гармоник частоты дискретизации (рис. 1.2, б). В результате модуляции создаются спектр исходного аналогового сигнала и две боковые полосы около каждой дискретной частоты в спектре импульсной последовательности (рис. 1.2, в).

Исходный сигнал восстанавливается с помощью фильтра нижних частот, рассчитанного на подавление всех частот кроме частот исходного сигнала. Как показано на рис. 1.2, восстанавливающий фильтр нижних частот должен иметь частоту среза, которая расположена  между  w_в и  w_д - w_в.  Следовательно, разделение  возможно  только в том случае, если w_д - w_в больше, чем w_в, т.е. если w_д > 2 ´ w_в.

 

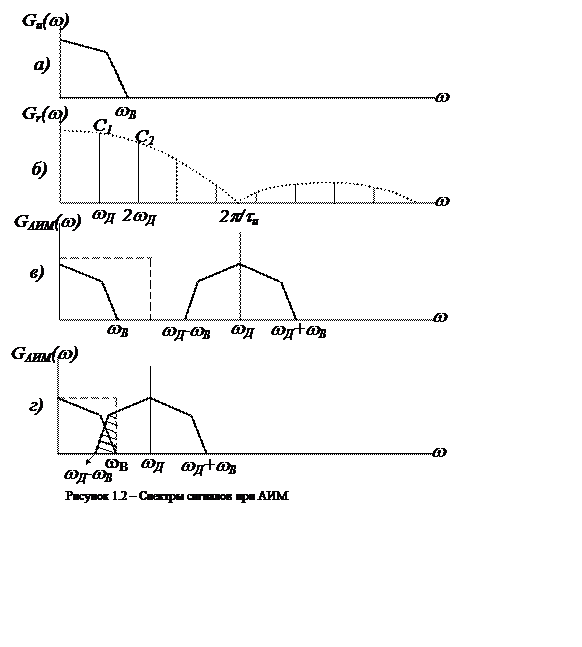Если же входной непрерывный сигнал дискретизируется с частотой w_д < 2 ´ w_в, то он не может быть восстановлен без искажений. Как показано на рисунке 1.2г, искажения в выходном сигнале возникают вследствие того, что нижняя боковая полоса частоты дискретизации попадает в исходный спектр и не может быть выделена из него путем фильтрации.

Полученный аналоговый АИМ сигнал u_АИМ(iT_д) (рисунок 1.1) перед преобразованием в цифровой сигнал подвергается операции квантования, которая заключается в замене бесконечного множества значений напряжения сигнала u_АИМ(iT_д) конечным множеством дискретных (квантованных) значений u_кв(iT_д) u₁,u₂,u₃,u₄  и т.д. рисунке 1.3.

 

Расстояние между ближайшими разрешенными уровнями квантования D называется шагом квантования. Шкала квантования называется равномерной, если все шаги квантования равны между собой. Если амплитуда импульса i-го отсчета удовлетворяет условию