

1.1.34 Основные виды матриц графовых моделей сетей (определение, примеры, информационное содержание для практического применения в проектировании)
При проектировании с ЭВМ нужно ввести информацию наиболее приемлемым способом, т.е главное место отводится математическому моделированию, при проектировании телекомммуни кац –х сетей, наиболее удобно использовать матем. Модели виде графов, что дает обширный математический аппарат –называется теория Графа
Граф – пара множеств (множество вершин и множество ребер, а также отображения) которые устанавливают связь или связи между этими множествами.
G- обозн. графа. G= (U;X;) практически граф выглядит как совокупность точек на плоскости, которые обозначают, какие-то объекты (вершины) и соединяются между собой отрезками линий- которые назыв. ребрами. В нашем случае вершинами являются пункты связи, станции, выносы с АТС, а ребра участки кабельных линий.
X – множество вершин. X = { х1,х2,…хn}. X € хi ; ver . рисунок?
U – множество ребер. U = { u1,u2,…un}. U € uj; reb.
φ - отображение φ : X --- U;( отображение множества вершин и ребер ) взаимооднозначное.
Представление графа: 1)вербальное (словесное) ; 2)в виде матриц; 3)геометрическое( в виде рисунка); 4) FO – представление графа в виде множеств; 5) теоретико-множественное и.т.д;
У каждой вершины может быть вес, число целое или рациональное , которое поставлено в соответствии данной вершине и и отображает стоимость, номерную емкость, пропускную способность.
α – вес ребра ,это число или несколько, которые поставлены в соответствии конкретному ребру и отражают длину, пропускную способность и т.д. Вершина X –инцидентна ребру U, это отношение принадлежности т.е вершина X принадлежит ребру U. Инцидентность –это отношение принадлежности. Верно в обратном случае подтверждение, что ребро инцидентно вершине.
Теоретико-множественное представление графа. х1,х2,х3.х4,х5,х6; u1,u2,u3.u4,…u7,х8;
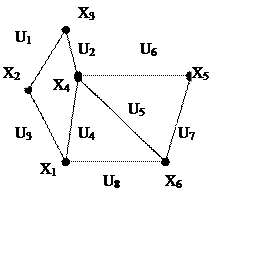 отображение
u1 — х1,х2; u2 — х3.х4; u3 — х1,х2; u4 — х1,х4; u5— х4,х6; u6 — х4,х5; u7 — х5,х6; u8 — х1,х6;
отображение
u1 — х1,х2; u2 — х3.х4; u3 — х1,х2; u4 — х1,х4; u5— х4,х6; u6 — х4,х5; u7 — х5,х6; u8 — х1,х6;
Матрицы смежности и инцидентности .
Две вершины назыв. смежными ,если они инцидентны одному и тому же ребру. 2 вершины смежны графовой модели, когда существует ребро графа инцидентное им обоим.
Матрица инцидентности графа G – это прямоугольная матрица вида М={mij}, где mij –элементы матрицы,они равны1когда вершина хi инцидентна ребру uj; графа G, u mij =0(тоже элемен матрицы) в ином случае. Матрица смежности
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
|
|
Х1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
Хi … |
1 |
0 |
1 |
0 |
0 |
0 |
|
Х6 |
Матрица инцидентности
|
U1 |
U2 |
U3 |
U4 |
U5 |
U6 |
U7 |
U8 |
|
|
Х1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
Хi … |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
м Х6 |
Матрица смежности – (матрица соседства, матрица смежных графов.) это квадратичная матрица А. состоит из элементов aj А={aij}, в aj=1,при xi смежными с хi, или aij=0 в противоположном случае.
Матрица расстояний. –(это матрица кратчайших цепей) , квадратная матрица D = { dij}, в которой каждый элемент D ij= ρ(ҳі, ҳј) .в графе G, если расстояние xj недостижимо xi, то ρ = бесконечности.
4




![]() X5
X4
X5
X4
2 3 3 5
![]() X1
X1
![]() 4
X2
4
X2
6 X3
Рисунок 2.
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Є(хі) |
|
|
Х1 |
0 |
4 |
10 |
6 |
2 |
10 |
|
Х2 |
4 |
0 |
6 |
3 |
3 |
6 |
|
Х3 |
10 |
6 |
0 |
5 |
9 |
10 |
|
Х4 |
6 |
3 |
5 |
0 |
4 |
6 |
|
Х5 |
2 |
3 |
9 |
4 |
0 |
9 |
экцентриситет вершины – это есть max расстояние от х до у ε(x) = max ρ(х.у) ,
у ЄX . вершины в графе G до наиболее удаленной вершины этого же G).
Диаметр графа . экцентриситет – это характеристика вершины.
Диаметр –это есть max экцентриситет вершин . d(G)= max ε(xі). xіЄХ. d = 10.
Радиус графа тоже является характеристикой всего графа r(G) = min ε(xі) ). xіЄХ.
Центр графа или центральная вершина,- это вершина, экцентриситет которой равен r.
Центров в графе может быть несколько . r.(G)= ε(x) x – центр.
Периферийная вершина в которой экцентриситет равен диаметру d(G)= max ε(х).
Цепь на которой достигаются значения диаметра, называется диаметральным.
От х1 до х3 .
В проектировании по заданным матрицам,содержание которых представляет информацию о расположении объектов относительно друг друга,расстоянии между объектами(в зависимости от вида матриц),можно представить графовую модель, отображающую структуру сети(число и примерное расположение пунктов связи, протяженность линий связи,стоимостные характеристики кабелей и другое).
Причем,имея только матрицу расстояний нельзя представить реально структуру сети.А только при условии,что матрица расстояний и матрица смежности совмещены.Где по информационной части можно определить и расстояние расположение объектов относительно друг друга.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.