![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ФИО, группа, дата
Задание №2
Решение СЛАУ методом итераций
Задание: Методом итераций решить систему линейных алгебраических уравнений
5х1 + х2 – х3 = 4 х1 + 5х2 – х3 = 8 х1 + 2х2 + 4х3 = 17
Результат получить с погрешностью å = 0.0001.
Создать приложение, которое может решать подобные системы. Алгоритм решения можно посмотреть в лекциях, если они у вас есть ;-))).
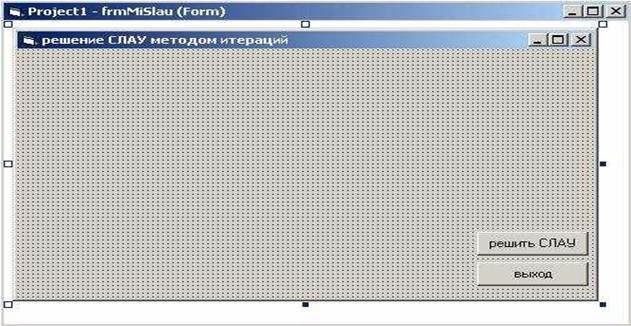
Примерный вид приложения показан ниже
На форме разместить всего два объекта: командную кнопку «решить СЛАУ» и командную кнопку «выход».
В таблице №1 перечислены объекты, их свойства и значения, которые устанавливаются первоначально.
Таблица №1
№ Объект
1 Форма (Form)
2 Кнопка (CommandButton)
3 Кнопка (CommandButton)
Свойство
Name
Caption
Name
Caption
Name
Caption
Значение
frmMiSlau решение СЛАУ методом bnthfwbq
btnCalc решить СЛАУ
btnStop выход
Перейдя в окно кодов с кнопкой «решить СЛАУ» свяжем процедуру:
Private Sub btnCalc_Click()
' решение СЛАУ n-го порядка методом итераций
' n- порядок системы
' открываем файлы для ввода и вывода
Open "d:\vb\vb\vvIn.txt" For Input As #1
Open "d:\vb\vb\vyvOut.txt" For Output As #2
' считываем данные из файла и объявляем массивы
Input #1, n, eps
ReDim a(n, n), b(n)
ReDim xk(n), x(n)
' Расширенная матрица системы (матрица системы
' вместе с правой частью) задается построчно в файле данных.
' !!!Матрица должна быть с диагональным преобладанием!!!
For i = 1 To n
For j = 1 To n
Input #1, a(i, j)
Next j
Input #1, b(i)
Next i
' преобразование матрицы к виду удобному для итераций
For i = 1 To n
dig = a(i, i)
b(i) = b(i) / dig
' сразу задаем нулевое приближение
x(i) = b(i)
For j = 1 To n
If i = j Then
a(i, i) = 0
Else
a(i, j) = -a(i, j) / dig
End If
Next j
Next i
' вывод нулевого приближения на форму и в файл
For i = 1 To n
Print "x("; i; ") = "; Format(x(i), "##.####"); " ";
Print #2, "x("; i; ") = "; Format(x(i), "##.####"); " ";
Next i
Print #2,
' вычисляем 1-ое приближение
Call miSLAU(a(), b(), x(), xk(), n)
' вывод очередного решения на форму и в файл
For i = 1 To n
Print "x("; i; ") = "; Format(xk(i), "##.####"); " ";
Print #2, "x("; i; ") = "; Format(xk(i), "##.####"); " ";
Next i
Print #2,
' находим наибольшее расстояние между приближениями
en = Abs(xk(1) - x(1))
For i = 2 To n
t = Abs(xk(i) - x(i))
If t > en Then en = t
Next i
' счетчик итераций
k = 1
' собственно итерационный процесс
Do While en > eps
' запоминаем предыдущее решение
For i = 1 To n
x(i) = xk(i)
Next i
' вычисляем новое приближение
Call miSLAU(a(), b(), x(), xk(), n)
' вывод очередного решения на форму и в файл
For i = 1 To n
Print "x("; i; ") = "; Format(x(i), "##.####"); " ";
Print #2, "x("; i; ") = "; Format(x(i), "##.####"); " ";
Next i
Print #2,
' находим наибольшее расстояние между приближениями
en = Abs(xk(1) - x(1))
For i = 2 To n
t = Abs(xk(i) - x(i))
If t > en Then en = t
Next i
k = k + 1
If k > 32 Then
Print "Требуемая точность не достигнута."
Print "Прошло 32 итерации "
Exit Do
End If
Loop
' вывод окончательного решения на форму и в файл
Print #2,
Print "Решение системы"
Print #2, "Решение системы"
For i = 1 To n
xiOut = Format(x(i), "##.#####")
Print "x("; i; ") = "; xiOut
Print #2, "x("; i; ") = "; xiOut
Next i
Close
End Sub
С кнопкой «Выход» свяжем процедуру
Private Sub btnStop_Click()
End
End Sub
В области General напишем подпрограмму
' метод итераций для СЛАУ
Sub miSLAU(a(), b(), x(), xk(), n)
For i = 1 To n
s = 0
For j = 1 To n
s = s + a(i, j) * x(j)
Next j
xk(i) = b(i) + s
Next i
End Sub
Сохранить форму у себя на диске N папке n:\numMtd\miSlau\ в файле под именем miSlau.frm и проект под именем proMiSlau.vbp
Прежде чем запускать проект на исполнение, Блокнотом создать файл исходных данных
3 0.0001
5 1 -1 4
1 5 -1 8
1 2 4 17 и сохранить его в папке n:\numMtd\miSlau\ под именем vvIn.txt.
В MS Word’e написать шапку, задание, собрать все процедуры, файл исходных данных и файл результатов расчета
Решение системы
x( 1 ) = ,99995
x( 2 ) = 1,99995
x( 3 ) = 3,00004 и вывести все это на печать.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.