Расчет тока через сопротивление методом эквивалентного генератора

Оглавление:

1.    Исходные данные. 2

2.    Расчет с использованием законов Кирхгофа. 3

3.    Проверку расчета по балансу мощности. 6

4.    Расчет методом контурных  токов. 7

5.    Расчет тока через сопротивление R методом эквивалентного генератора. 9

Литература: 12

1.  Исходные данные

Схема 13, Вариант 13,  R₂

Исходная электрическая схема

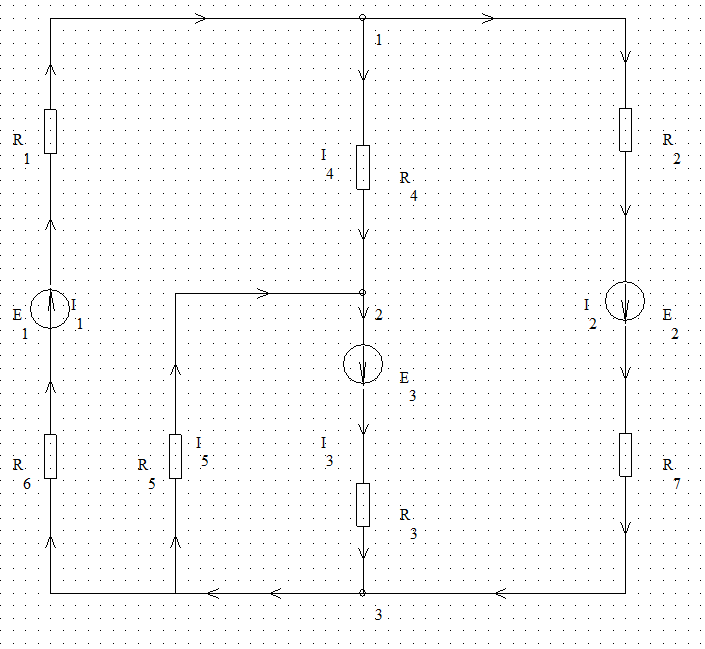
Рисунок 1

2.  Расчет с использованием законов Кирхгофа.

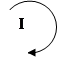
Рисунок 2

Всего в схеме  b = 5 ветвей.

Число узлов   y = 3.

Число неизвестных токов 5,

Число независимых уравнений, составляемых по первому закону Кирхгофа

y-1=3-1=2

Число независимых уравнений, составляемых по второму закону Кирхгофа

b-(y-1)=5-(3-1)=3

Выберем положительные направления токов и обозначим их стрелками.

Выберем и обозначим стрелками направления обхода трех независимых контуров:

I, II, III  (см .  рисунок  2)

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов  и контуров электрической цепи; при решении этих уравнений находятся неизвестные токи ветвей. Общее число уравнений должно быть равно числу неизвестных, т.е. числу ветвей цепи. Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, уменьшенному на единицу; остальные уравнения составляются по второму закону Кирхгофа.

Условно примем токи, оттекающие от узла со знаком «+», а подтекающие к узлу со знаком «-».

Дляузла  1

-I1+I2+I4=0

Дляузла  2

I3-I4-I5=0

Дляконтура  I:

I1·(R1+R6)+I4·R4-I5·R5=E1

Дляконтура  II:

I2·(R2+R7)-I3·R3-I4·R4=E2-E3

Для контура  III:

I3·R3+I5·R5=E3

В результате получим следующую систему уравнений для определения тока в ветвях:

-I1+I2+I4=0

I3-I4-I5=0

I1·(R1+R6)+I4·R4-I5·R5=E1

I2·(R2+R7)-I3·R3-I4·R4=E2-E3

I3·R3+I5·R5=E3

Подставим исходные данные в уравнение

-I1+I2+I4=0

I3-I4-I5=0

8I1+5I4-3I5=12                          (1)

8I2-4I3-5I4=8

4I3+3I5=8

Для решения системы линейных уравнений (1) составим матрицы «А» коэффициентов «B» свободных членов и найдем токи в программном комплексе «Mathcad»:

Искомые токи в ветвях схемы равны:

I1=1,817 А

I2=1,683 А

I3=1,200 А

I4=0,133 А

I5=1,067 А

3.  Проверку расчета по балансу мощности.

При  проверке баланса мощностей в тех ветвях цепи, где истинное направление тока совпадает с направлением  ЭДС, соответствующая ЭДС является источником энергии, а в тех случаях, когда направление ЭДС и тока противоположны, ЭДС – потребитель энергии.

Все сопротивления независимо от направления протекающего тока будут являться потребителями энергии. См. Рисунок 3

Рисунок 4

Рассчитаем общую мощность потребителей:

I²₁·R₆+I²₁·R₁+I²₂·R₂+I²₂·R₇+I²₃·R₃+I²₄·R₄+I²₅·R₅=17,5874+10,5524+13,1951+7,91706+5,47523+0,0199972+3,67448=58,421 Вт

Рассчитаем общую мощность источников:

E₁·I₁+E₂·I₂+E₃·I₃=23+26+9,4=58,400 Вт

Баланссходится.

4.  Расчет методом контурных  токов

Выберем направления контурных токов, которые обозначим  .

Составим систему уравнений для контуров (Рисунок 4)

Рисунок 5

При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток (I₁₁, I₂₂, I₃₃) равный току в независимой ветви соответствующего контура, положительное направление которого указывается стрелкой произвольно. Число уравнений b-y+1=5-3+1=3.

Составляем уравнения для всех контуров в общем виде:

I11·R11+I22·R12+I33·R13=E11

I11·R21+I22·R22+I33·R23=E22

I11·R31+I22·R32+I33·R33=E33

где, собственные (полные) сопротивления контуров 1,2,3 соответственно:

Смежные сопротивления между контурами:

R11=R1+R6+R4+R5=3+5+3+5=16 Ом

R22=R2+R7+R3+R4=3+4+5+3=17 Ом

R33=R3+R5=4+3=7 Ом

Контурные ЭДС 1,2,3 контуров соответственно равны:

R12=-R4=-5 Ом

R13=-R5=-3 Ом

R21=-R4=-5 Ом

R23=-R3=-4 Ом

R31=-R5=-3 Ом

R32=-R3=-4 Ом

Подставим численные значения в общее уравнения для всех контуров и составим систему уравнений в матричной форме:

16I11-5I22-3I33=12

-5I11+17I22-4I33=8                     (2)

-3I11-4I22+7I33=8

Для решения системы линейных уравнений (2) составим матрицы «А» коэффициентов «B» свободных членов и найдем токи в программном комплексе «Mathcad»:

Решая систему уравнений, получим:

I11=1,817 А

I22=1,683 А

I33=2,883 А

Найдем токи в ветвях:

I1= I11=1,817 А

I2= I22=1,683 А

I3=-I22+I33=1,2 А

I4= I11-I22=0,133 А

I5=-I11+I33=1,067 А

5.  Расчет тока через сопротивление R методом эквивалентного генератора

Для расчета электрической цепи методом эквивалентного генератора необходимо:

§  разомкнуть интересующую нас ветвь (ветвь 2)

§  любым методом определить напряжение холостого хода на разомкнутых зажимах

§  определить входное сопротивление разомкнутых зажимов, предварительно исключив из схемы все источники (Ист. ЭДС закоротить, Ист. тока разомкнуть).

Рисунок 5

Разомкнем ветвь 1-3:

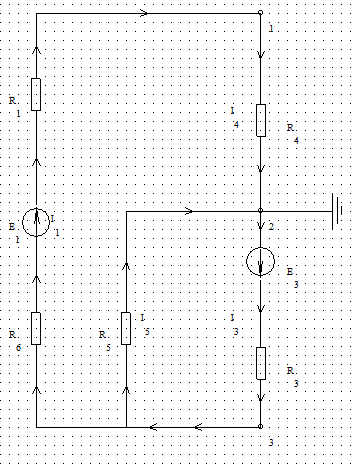
Рисунок 5.1

Для нахождения U_xx  найдем потенциалы узлов 1-3 (предварительно приняв потенциал узла «2» равным нулю) методом узловых потенциалов:

Общее уравнение имеет вид:

j1·G11+j3·G13=I11

j1·G31+j3·G33=I33

Собственные и  общие проводимости:

G11=1/(R1+R6)+1/R4=0,325

G13=-1/(R1+R6)=-0,125

G33=1/(R1+R6)+1/R3+1/R5=0,708333

Узловые токи:

I11=E1/(R1+R6)=1,5

I33=-E1/(R1+R6)+E3/R3=0,5

Получили систему линейных уравнений:

0,325j1-0,125j3=1,5

-0,125j1+0,70833j3=0,5

Для решения системы линейных уравнений (3) составим матрицы «А» коэффициентов «B» свободных членов и найдем узловые