















ЛАБОРАТОРНАЯ РАБОТА №7 (ЛР7)
КОДИРУЮЩИЕ УСТРОЙСТВА ЦИКЛИЧЕСКИХ КОДОВ
ЦЕЛЬ РАБОТЫ: изучение принципов построения и исследование работы кодеров циклических (n, к) – кодов, применяемых в системах телемеханики.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Циклическим кодом называется линейный систематический код, который вместе с любым своим кодовым слоем содержит и его циклический сдвиг.
Основными устройствами, используемыми при кодировании и декодировании циклических кодов, являются регистры сдвига с логическими связями (линейные переключательные схемы) , осуществляющие как умножение, так и деление многочленов.
При кодировании из источника поступают блоки из К информационных символов (а 1, а 2 … а к), которые передаются в канал связи и дополняются r проверочными символами (в 1, в 2 … в). Таким образом, каждому блоку из К информационных символов в кодирующем устройстве сопоставляется n-разрядный кодовый вектор
V = (а 1, а 2 … а к , в 1 … в r ) .
Лабораторный стенд позволяет изучить работу кодирующих устройств как полных , так и укороченных кодов при применении двух способов построения кодовых комбинаций. Оба способа порождают одни и те же кодовые слова.
1. Кодирование циклических кодов методом деления информационных символов на образующий многочлен
Алгоритм кодирования циклического кода, использующий данный метод, предусматривает вычисление проверочных символов как получение остатка r (х) от деления многочлена а (х)* х r на образующий многочлен g (х), где а (х) – многочлен, соответствующий произвольной информационной последовательности на входе кодирующего устройства. Разрешённая кодовая комбинация циклического кода получается путём добавления остатка r (х) к кодовой комбинации простого кода а (х), т.е. V (х) = а (х)* х r + r(x).
Совокупность кодовых комбинаций циклического (n, к ) – кода может быть представлена образующей матрицей G = [ I k; R], где
I k – единичная матрица размерности ( к × к ),
R - матрица остатков, размерность которой ( к × r ).
Для вычисления остатков используются схемы деления на фиксированный многочлен g (x) (лабораторная работа №6). В кодирующем устройстве наиболее целесообразно использование схем, совмещающих операции умножения на одночлен х r и деления на g(x), что позволяет вычислить значение проверочных символов (остаток) за К тактов.
Кодирующее устройство, использующее подобную схему деления, представлено на рис. 7.1, образующий многочлен g(х) = х 3 + х 2 +1. Схема деления состоит из r = 3 ячеек памяти (П1 – П3) и двух сумматоров по модулю два. На вход устройства подаётся произвольная последовательность К - разрядного неизбыточного кода, начиная с коэффициентов старших разрядов.
В исходном состоянии все ячейки памяти находятся в состоянии “0”, конъюнкторы 1 и 3 открыты, а элемент 2 закрыт. Информационные символы одновременно поступают как в канал связи (с выхода), так и в регистр деления , где за 4 такта формируется остаток , т.е. проверочные разряды в 1, в 2 , в 3 . Затем конъюкторы 1 и 3 закрываются, а элемент 2 открывается и за следующие 3 такта проверочные элементы выводятся в канал связи. Переключение элементов 1, 2, 3 осуществляется от блока управления, который на схеме не показан.
Напомним, что неприводимый многочлен g (х) = х 3 + х + 1 образует полный циклический код (7, 4)-код, матрица которого:
G (7, 4) = 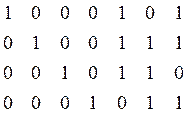
2. Кодирование циклических кодов методом вычисления проверочных символов как результат проведения линейных операций.
Поскольку циклический код относится к линейному коду , то значение его проверочных разрядов в 1, в 2 , в 3 . . . могут быть определены в результате проведения линейных операций над известными информационными разрядами. Однако, в силу свойств цикличности кода достаточно определить линейную операцию только для одного проверочного элемента. Эта операция целиком задаётся проверочным полиномом:
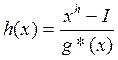
где g *( х ) – многочлен, сопряжённый с образующим многочленом g ( х ).
Определив в 1 и произведя циклический сдвиг , получаем кодовое слово, которое также относится к циклическому коду. По элементам этой комбинации теперь вычисляется следующий проверочный элемент, опять производится циклический сдвиг и т.д. Следовательно , для формирования кодовых комбинаций циклического кода необходимо иметь устройство, которое в соответствии с многочленом h ( х ) вычисляет в i по известным значениям информационных элементов.
Пусть циклический (7, 4)– код опять задан многочленом
g ( х ) = х 3 + х + 1. Тогда сопряжённый многочлен g*(х) =
= х 3(х -3 + х -1 + 1)=х 3 + х 2 + 1, проверочный полином п х = х 4+х 3+ х 2 +1, а соответствующее ему линейное уравнение в 1 = а 1 + а 2 + а 3.
Кодирующее устройство (рис. 7.2) строится на основе К - разрядного регистра сдвига. Выходы ячеек памяти подключаются к сумматорам по модулю 2 в соответствии с вышеприведённым линейным уравнением. В исходном состоянии конъюнктор открыт, а элемент 2 находится в закрытом состоянии. За первые К – тактов, поступающие на вход, информационные символы заполняют ячейки регистра. Причём старший разряд а1 достигает ячейки П1. Затем элемент 1 отключается, а элемент 2 открывается. На каждом из последующих тактов один информационный символ выдаётся на выход схемы (в канал связи) и одновременно по цепи обратной связи формируется один проверочный разряд.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.