Кодирующие устройства циклических кодов (Лабораторная работа № 7), страница 6

При использовании того же регистра деления, что применяется при кодировании (назовем его схемой деления второго типа), соответствие между векторами ошибок и остатками на n такте будет иное. Теперь вместо вычисления синдрома полинома U (x) определяется синдром полинома х^r U (x) (по модулю g (x)), что равносильно, как указывалось выше, нахождению остатка от деления х^r на g (x). Так, если ошибка появилась в старшем разряде  = х⁶, то остаток от деления х⁶⁺³ = х⁹ на g (x) = х³ + х + 1 равен х², что в двоичном представлении – 100.

Табл. 8.2. является таблицей декодирования рассматриваемого выше кода при применении схемы деления 2-го типа.

Таблица 8.2.

На рис. 8.3 представлена схема декодирующего устройства, отвечающая данной таблице декодирования. ДО выделяет синдром 100, т.е. реализует логическую функцию у =  авс.

При декодировании кодов с d_мин = 4 все одиночные ошибки исправляются, а ошибки второй кратности обнаруживаются. Функционирование устройства в том случае отличается от рассмотренного выше тем, что при появлении в конце цикла коррекции остатка отличного от нуля, информация, записанная в выходном регистре, уничтожается. В схеме модуля стирание информации при обнаружении неисправляемых ошибок осуществляется на 2-м такте. Если остаток нулевой, то содержимое Вых.Р сохраняется.

Схема соответствующего устройства представлена на рис. 8.4. Она составлена для (7, 3)- кода, образующего многочлен

g (x) = x⁴ + x³ + x² + 1.

Декодирование укороченных кодов

Для декодирования укороченных кодов возможно использовать аппаратуру полных циклических кодов при условии, что каждой укороченной комбинации предпосылается i нулей. Цикл декодирования укороченного кода при этом займет не n-i такт, а все n тактов.

Декодирование, однако, можно осуществлять быстрее, если в генераторе синдрома одновременно с делением на g (x) производить операцию умножения на хⁱ. Тогда вместо вычисления синдрома U (x) будет вычисляться синдром полинома хⁱ U (x) (по модулю g (x)), что равносильно нахождению остатка от деления хⁱ  на g (x). Эта операция позволяет сократить нахождение выделяемого синдрома на 2 i тактов (за два цикла).

В качестве примера рассмотрим построение декодирующего устройства укороченного (6, 3) – кода, g (x) = x³ + x + 1.

Укорочение кода на один информационный символ равносильно исключению из образующей матрицы (7, 4) – кода первой строки и левого столбца. Соответственно, для рассматриваемого кода:

G_{(6,  3)} =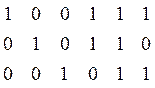

Если в регистре деления будем производить одновременно операцию предварительного умножения на х¹ и деления на g (x), то выявленным синдромом опять явиться синдром 101, а нахождение его осуществляется за n – 1 = 6 тактов. Действительно, пусть вектор ошибки 100000 (искажен старший разряд), т.е.   = х⁵. Тогда содержимое РД будет отвечать делению многочлена х¹   = х⁶.                           

Из табл. 8.1. видно, что одночлену  х⁶  принадлежит остаток 101. вектору ошибки 010000 теперь соответствует остаток от деления х¹х⁴=х⁵ , т.е. остаток 111. Рассуждая дальше подобным образом, можно построить таблицу декодирования для (6, 3) – кода.

Схема декодирующего устройства представлена на рис. 8.5. Схема ориентирована на элементную базу лабораторного модуля.