Parametric transfer functions of feedback multirate systems with disturbance acting on a continuous-time element, страница 3

To find the PTF's W_gy(s, t) and W_gu(s, t), we assume that g(t) = e^st. Since the system in Fig. 1 is linear, by definition [1] we have

                                                                           (21)

The signal y(t) passes through feedback loop through sampling elements and elements C₂(s), L(s), C₁(s), W(s), and F(s). Due to the stroboscopic property of sampling elements

                    (22)

Comparing (21) with the second equation in (22), we find

                                                     (23)

Since W_gy(s, 0)is continuous with respect to t, for t = 0 the equation (23) appears as

                                                       (24)

Solving (24) for W_gy(s, 0), we obtain

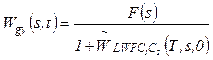                                                                 (25)

Substituting (25) into (23) gives

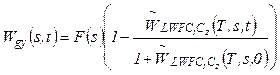                                                         (26)

It is directly verified that (26) solves the functional equation (23). Indeed, substituting (26) in (23), we obtain an identity.

Using similar reasoning, it is also possible to find a closed-form expression for the PTF W_gu(s, t). By definition,

                                                                         (27)

Substituting (27) into the first equation in (22), after reduction we obtain

                                                         (28)

Substituting (25) into the last equation and using continuity with respect to t, we finally obtain

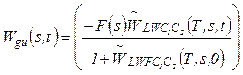                                                         (29)

Substituting (29) into (28), we obtain identity. Hence, the function (29) solves the functional equation (28).

Application of the PTF's (26) and (29) makes it possible to extend many investigation methods developed for sampled-data systems with a single sampling unit onto multirate systems. Some of them are realized in the toolbox [4] for Matlab.

6. CONCLUSION

Closed-form expressions are derived for parametric transfer functions of feedback multirate sampled-data systems for the case when disturbance acts directly at a continuous-time element. Using these results, it is possible to generalize many analysis and design methods developed for sampled-data systems with a single sampling unit onto multirate systems.

7. REFERENCES

[1] E. Rosenwasser, B.P. Lampe, Computer-Controlled Systems: Analysis and Design with Process-orientated Models, Springer Verlag, London, 2000.

[2] B. P. Lampe, V. O. Rybinskii, The estimation accuracy of digital control systems at the incomplete information about stochastic input disturbance, Rostock, Universitaet, 2000.

[3] V. O. Rybinskii, Robust stabilization of linear periodic systems. // V conference for yang scientist, 'Electropribor' research institute, SPb, 2002.

[4] V.O. Rybinskii, B.P. Lampe, and E.N. Rosenwasser Design of digital ship motion control with guaranteed performance. Proc. 49. Int. Wiss. Kolloquium, volume 1, pages 381 - 386, Ilmenau, Germany, 2004

[5] Rybinskii, V. Lampe, B.P. Rosenwasser, E.N GarSD - a Matlab toolbox for analysis and design of sampled-data systems with guaranteed performance // Proc. 49th IWK, Ilmenau, Germany, 2004