Parametric transfer functions of feedback multirate systems with disturbance acting on a continuous-time element, страница 2

                                                                (8)

where

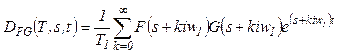                                                (9)

In (9), 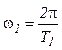, and G(s) is the TF of the (zero-order) hold. The closed-form expressions for the DTF (8) are given in [1]. The essense of the decomposition consist in a representation of the DTF  with period T₁ via periodic function  with period NT₁. In this case, for the DTF (8) we have

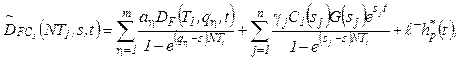
                           (10)

                           (11)

In (10) and (11) the following notation is used: q_h (h = 1,…,m) are poles of the function C₁(s), a_h are residues of the function C₁(s) at the poles q_h, and  is the transient response of the continuous element F(s), which is given by the formula

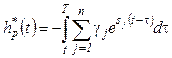
Accordingly, the PTF  of the system in Fig. 2 can be decomposed as

                                                            (12)

Using the terminology of [1], we shall call the representation (12) a decomposition of parametrical transfer function for the open-loop sampled-data system.

Since the function F(s) is strictly proper, the PTF  is continuous with respect to t.

4. PTF FOR OPEN-LOOP MULTIRATE SYSTEMS

Using the decomposition operation, it is possible to derive an expression for the PTF of the open-loop multirate systems shown in Fig. 3.

Here notation is similar to the previous cases. In the case under consideration, when T₂ = NT₁, thesystem in Fig. 3 will be called ascending [1].

Then, we find the PTF  for the system in Fig. 3. Since the system is linear, to find its PTF we take . Then, by definition

                                                                 (13)

Figure 3: Open-loop multirate sampled-data system

On the other hand,

                                                                           (14)

where

                                                      (15)

Due to the generalized stroboscopic effect, (15) can be rewritten as

                                                 (16)

Substituting (16) into (14), we obtain

                                               (17)

Comparing (17) and (13), we find that the PTF is defined by

                                      (18)

In (18), the functions  are defined as

                                   (19)

where  is the TF of the open-loop sampled-data system, consisting of a controller C₂(s), zero-order hold, and a continuous-time element L(s). Moreover,  is the representation (10), (11) for the DTF .

It should be noted that the function  is continuous with respect to t.

5. PARAMETRICAL TRANSFER OF THE FEEDBACK SYSTEM

Using (18), it is possible to derive the PTF's of feedback multirate system in Fig. 1 from input g(t) to outputs y(t) and u(t).

The system in Fig. 1 is periodic with period T₂. Therefore, the PTF's W_gy(s, t) and W_gu(s, t) are also periodic functions such that

                                             (20)

Moreover, since the functions F(s) and W(s) L(s) are strictly proper, the PTF's W_gy(s, t) and W_gu(s, t) are continuous with respect to t.