



MOBILE ROBOT CONTROL SYSTEM DESIGN BASED ON FUZZY NEURAL NETWORKS
Andrey V. Lyamin, Alena V. Rusak
Department of Computer Educational Technologies
Saint-Petersburg State University of Information Technologies, Mechanics and Optics
Kronverksky av. 49, Saint-Petersburg, 197101, RUSSIA
Tel: +7(812) 2325914, E-mail: alena@cde.ifmo.ru
Abstract - This paper presents a mobile robot control system design when desired motion trajectory is not well defined. The solution of the problem is based on use of neural networks and fuzzy logic. The hierarchical structure of control system with the fuzzy neural controller is obtained. It allows to use methods of the coordinating control for the design of motion algorithms at the low level of the control system.
This paper is devoted to the problems of a mobile robot control in case when the desired trajectory is a sequence of operations or points, i.e. an explicit description of a trajectory is absent. Example of the problem is a control of a mobile robot, which is moving in an environment with light beacons. The beacons are switched by a computer program. It allows to formulate the motion tasks of various complexity: direct motion to a beacon, motion between a group of active beacons [1, 2]. Complexity of the problem consists that
· there is no explicit description of the desirable trajectory;
· the robot is moving in an environment with uncertainties.
On the other side, fuzzy logic and neural networks are using when control tasks are not well defined. A combination of the fuzzy logic and the neural networks allows to get advantages of these approaches and to avoid of theirs defects. Quality of the fuzzy controller depends on a correct choice of a membership function. After training we can use the neural network for optimization of parameters of the membership function.
The mobile robot is a three-wheeled vehicle with two drive wheels. There are various type sensors on the moving platform, which are intended for the measuring of velocities and the recognition of configuration space [1, 3]. The robot estimates relative positions of beacons in configuration space. A priori positions of the beacons are unknown. A desired trajectory of robot motion is generated by combination of the beacons. We dedicated three primitives of the robot motion:
· the motion to the beacon along a straight line;
· the passage between two beacons along a straight line;
· the motion around of the beacon along an arc.
The second motion is similar to the first motion, but the robot must move between two beacons. Therefore, we shall be considering only the first and the third motions because of any a complex motion can be presented by a combination of these two primitives.
It is necessary to design an algorithm, which realizes identification of the current motion task and switches a local algorithm according with a situation. In this case, for design of local algorithms we can use methods of coordinating control. The hierarchical control system has been developed for the solution of this problem [1, 4]. The height level algorithm is realized by a logic block. Its goals are the definition of the current task type and the planning of the robot motion. The outputs of logic block are following parameters of the motion:
· DV is a constant;
· d is an angular deviation.
The DV equals to zero when the robot has to move along a straight line and the DV does not equals to zero when the desired motion is an arc.
HEIGHT-LEVEL LOGIC BLOCK
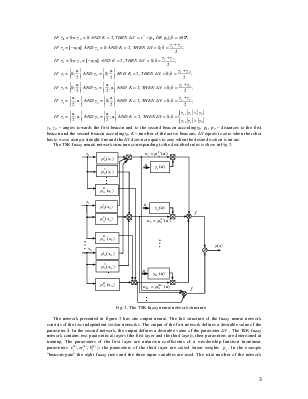
The logic block is realized by a fuzzy neural network. The feature of fuzzy neural networks is the use of fuzzy rules of conclusion for calculation of an output signal. Unlike classical neural networks in the fuzzy neural networks an adaptive choice of parameters of a fuzzification function is performed.
A fuzzy controller allows to solve problems by means of a fuzzy rules "if - then", which are assigned by an expert. Input data is information from the sensors of the technical vision system (signals about position of a beacons (ri,gi)), the desired motion parameters DV and d are defined on the output. The fuzzy rules are designed for each task ("gate", "figure of eight" and others).
The fuzzy neural network structure was developed on the base of two models: Takagi-Sugeno-Kang (TSK) model and Wang-Mendel model.
The generalized scheme of conclusion of Takagi-Sugeno-Kang model with using of M rules and of N variables xi has the following view [5]:
IF (x1 IS ![]() ) AND (x2 IS
) AND (x2 IS ![]() ) AND … AND (xN
IS
) AND … AND (xN
IS ![]() ), THEN
), THEN ![]() ,
,
…
IF (x1
IS ![]() ) AND (x2 IS
) AND (x2 IS ![]() ) ADN … AND (xN
IS
) ADN … AND (xN
IS ![]() ), THEN
), THEN ![]() ,
,
where ![]() is values of a corresponding membership coefficient
is values of a corresponding membership coefficient ![]() ,
, ![]() is a deterministic function
is a deterministic function
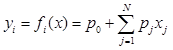 (1)
(1)
Here coefficients![]() are weights which are defined at training of the network.
are weights which are defined at training of the network.
The condition "IF ![]() IS
IS ![]() " is realized by a fuzzification function. In our paper, the
fuzzification function is presented by a generalized Gauss function separately
for each variable
" is realized by a fuzzification function. In our paper, the
fuzzification function is presented by a generalized Gauss function separately
for each variable![]() :
:
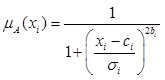 , (2)
, (2)
where ![]() is the operator
is the operator ![]() . The generalized Gauss function defines the standard Gauss function (b
= 1), the triangular function (b = 0.6) or the trapezoidal function. It
depends on the value of parameter b.
. The generalized Gauss function defines the standard Gauss function (b
= 1), the triangular function (b = 0.6) or the trapezoidal function. It
depends on the value of parameter b.
A membership function for the k-th conclusion rule can be written as
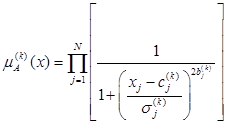 . (3)
. (3)
If M conclusion rules are used in the TSK model, a system output is defined as their average weighted and can be written as
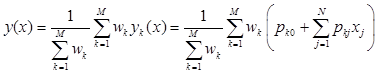 . (4)
. (4)
The weights ![]() are interpreted as importance of the components
are interpreted as importance of the components ![]() , which had been defined above.
, which had been defined above.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.