Релейные системы. Изучение нелинейных систем 2-го порядка, содержащих объект управления и релейный регулятор

Санкт-Петербургский Государственный Университет Информационных Технологий Механики и Оптики

Кафедра Систем Управления и Информатики

Лабораторная работа №3

«Релейные системы»

                                                                                            Выполнил:   Годгильдиев А,

Пронин В.

                                                                                                                          группа 4145

                                                                                        Проверил:    Пыркин А.А

Санкт-Петербург

2008

Цель работы: Рассмотреть нелинейные системы 2-го порядка, содержащие объект управления и релейный регулятор.

Объект управления:

,  x₁(0)=x₁₀       

,  x₂(0)=x₂₀

Регулятор: u = f₂(x₁, x₂)

1. Уравнения фазовых траекторий объекта управления, при постоянных значениях управления:

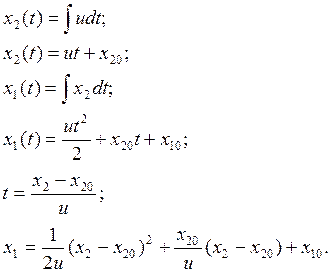
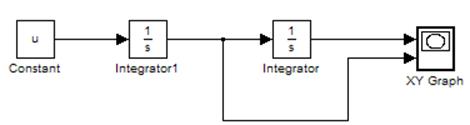
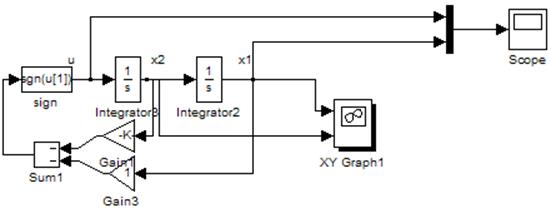
Схема моделирования:

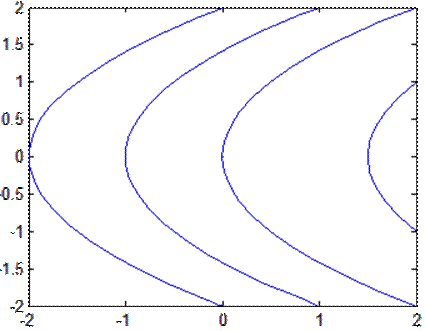
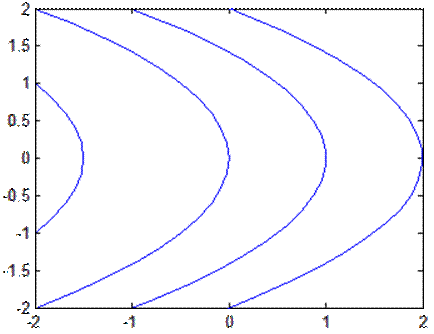
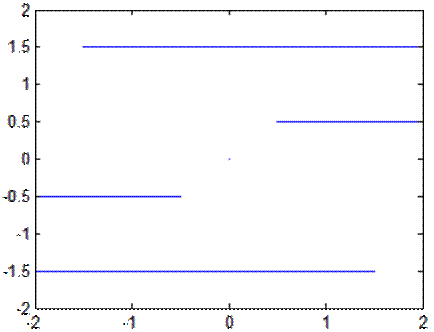
Фазовые траектории при u=-1

2. Метод припасовывания

f₂(x₁, x₂)= - sign (k₁ x₁ + k₂ x₂);

k₁=1; k₂=0,25.

k₁x₁ + k₂ x₂=0 – линия переключения

k₁ x₁ + k₂ x₂<0 – R⁺

k₁ x₁ + k₂ x₂>0 – R^-

Схема моделирования:

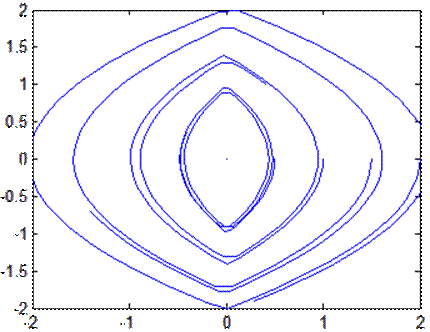
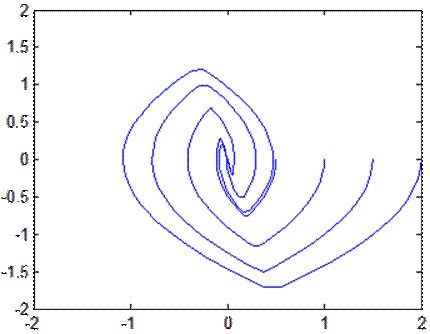      Фазовый портрет при k₂=0,25                                                  Фазовый портрет при k₂=0

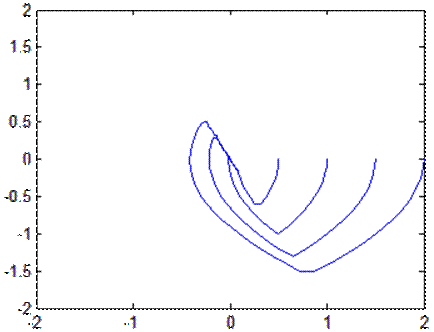
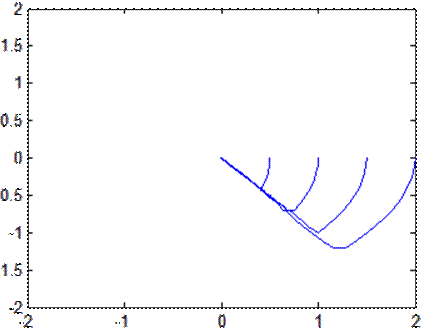   Фазовый портрет при k₂=0, 5                                                      Фазовый портрет при k₂=1

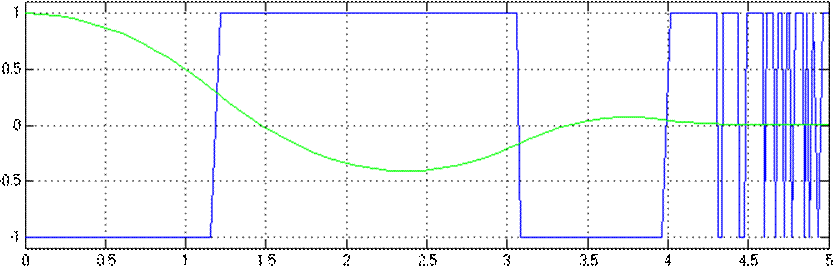
Графики переходных процессов х₁(t) и u(t) при k₂=0,25

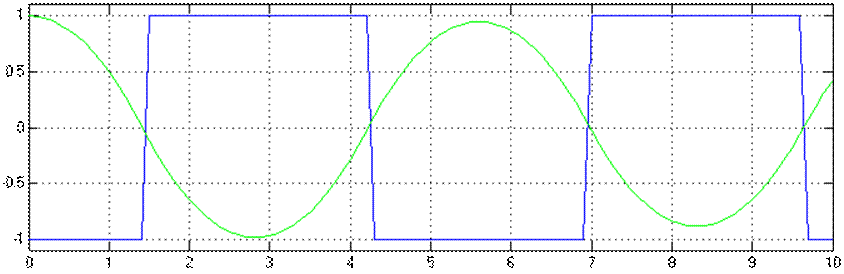
Графики переходных процессов х₁(t) и u(t) при k₂=0

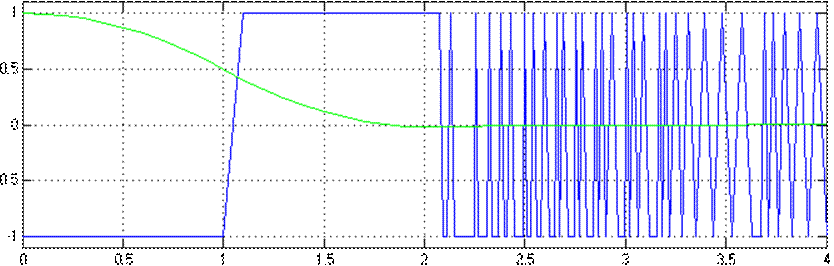
Графики переходных процессов х₁(t) и u(t) при k₂=0,5

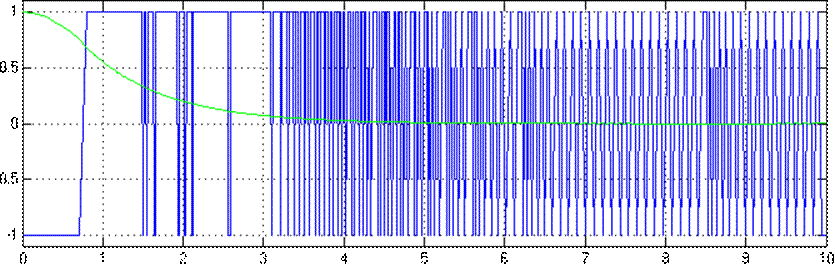 Графики переходных процессов х₁(t) и u(t) при k₂=1

3. релейная система c зоной нечувствительности, d=0.2

 .

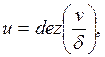
Так как функция  принимает три постоянных значения -1, 0, 1, то на интервалах знакопостоянства система линейна.

Области знакопостоянства:

 

  - зона нечувствительности

 ,

Линии переключения ():

 ,

 ,

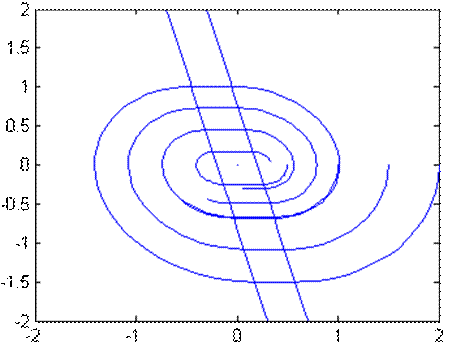
Фазовый портрет при k₁=1, k₂=0,25

 .

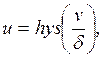
Так как функция  принимает два постоянных значения -1 и 1, то на интервалах знакопостоянства система линейна.

Области знакопостоянства:

, при ,

, при .

Линии переключения ():

  при ,

 при ,

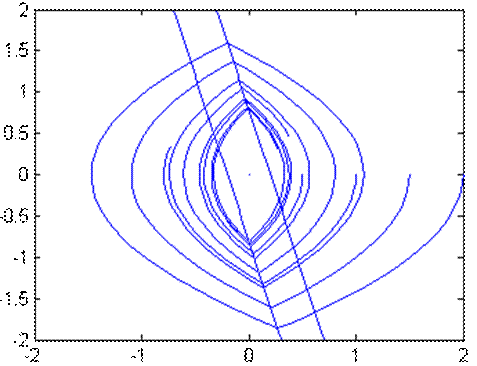
Фазовый портрет при k₁=1, k₂=0,25

Вывод: в данной работе были рассмотрены нелинейные системы 2-го порядка, содержащие объект управления и релейный регулятор, с помощью метода припасовывания построены их фазовые портреты.