











МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ МЕХАНИКИ И
ОПТИКИ
|
Кафедра |
Систем Управления и Информатики |
Группа |
5147 |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к расчетной работе
|
По курсу адаптивных и робастных систем (часть 1 Теория чувствительности систем управления) |
|
Автор курсового проекта |
Васильев В. И. |
(подпись) |
|
|
(фамилия, и.о.) |
|||
|
Руководитель |
Ушаков А. В. |
(подпись) |
|
|
(фамилия, и.о.) |
|||
1б, 2б, 3а, 4а, 5б, 6б, 7в
|
“ |
5 |
“ |
декабря |
20 |
07 |
г. Санкт-Петербург, 200 |
7 |
г. |
|
Курсовой проект выполнен с оценкой |
||||||||
|
Дата защиты “ |
“ |
20 |
г. |
|||||
|
Содержание:1 Построение МТЧ непрерывного ОУ. Ранжирование параметров…..........................3 2 Построение МТЧ дискретного ОУ к вариации интервала дискретности.….............5 3 Построение МТЧ спроектированной системы по каждому из параметров...........................................................................................................................6 4 Построение матрицы функций модальной чувствительности и выделение неблагоприятного сочетания вариаций параметров.....................................................11 5 Построение закона управления для объекта, заданного интервальными элементами…………………………………………………………………………..…..12 Заключение....................................................................................................................... 14 Литература.........................................................................................................................15 |
|||||||||||||||||
КСУИ.1165147.001 ПЗ |
|||||||||||||||||
|
Изм |
Лист |
№ док |
Подпись |
Дата |
|||||||||||||
|
Разработал |
Васильев В |
Расчетная работа по курсу адаптивных и робастных систем Пояснительная записка |
Литера |
Лист |
Листов |
||||||||||||
|
Проверил |
Ушаков АВ |
2 |
15 |
||||||||||||||
|
Н.Контроль |
|||||||||||||||||
|
Утвердил |
|||||||||||||||||
|
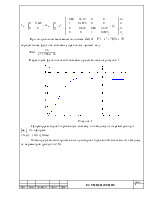
1 Построение МТЧ непрерывного ОУ. Ранжирование параметров Дана передаточная функция «вход-выход (ВВ)» НОУ:
Перейдем к канонической наблюдаемой форме.
Матрицы номинального ОУ:
Построение семейства моделей траекторной чувствительности:
и формирование семейства агрегированных систем:
где |
|||||||||||||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
||||||||||||||||
|
3 |
|||||||||||||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
|||||||||||||
|
Вычислим матрицы управляемости по функции траекторной чувствительности и их нормы:
Проранжируем параметры по потенциальной чувствительности:
|
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
4 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
2 Построение МТЧ дискретного ОУ к вариации интервала дискретности Векторно-матричное описание дискретного объекта управления имеет вид:
где:
Для модели траекторной чувствительности получим представление:
Матрицы номинального дискретного ОУ имеют вид:
Матрицы моделей траекторной чувствительности имеют вид:
Матрицы агрегируемой системы:
Составим матрицу управляемости агрегированной системы:
|
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
5 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
3 Построение МТЧ спроектированной системы по каждому из параметров Имеем:
Закон управления имеет вид:
ОУ агрегируется с ЗУ, образуя систему:
Из требований к проектируемой системе найдем матрицы F(q), G(q), K, Kg.
Учитывая, что
Отсюда получаем:
Найдем матрицу F и F(q):
Математическая запись закона управления:
|
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
6 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
Найдем G(q):
Построение семейства моделей траекторной чувствительности:
и формирование семейства агрегированных систем:
где
|
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
7 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
При полученном желаемом полиноме
Переходная функция такой системы представлена на рисунке 1.
Рисунок 1. Сформируем
спроектированную систему по каждому из параметров при
Ниже представлены кривые выходов спроектированной системы по каждому из параметров (рисунки 2-6). |
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
8 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
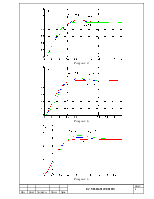
Рисунок 2.
Рисунок 3.
Рисунок 4. |
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
9 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
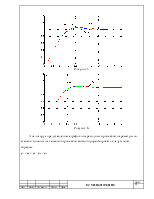
Рисунок 5
Рисунок 6. Анализируя представленные графики переходных процессов, параметры по степени влияния на качество процессов можно проранжировать следующим образом:
|
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
10 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
4 Построение матрицы функций модальной чувствительности и выделение неблагоприятного сочетания вариаций параметров.
Запишем
матрицу
Вычислим
функции модальной чувствительности
и сконструируем матрицу функций модальной чувствительности в виде функций чувствительности вещественной и мнимой частей:
Построим
сингулярное разложение для матрицы
Правые сингулярные векторы
|
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
11 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
5 Построение закона управления для объекта, заданного интервальными элементами. Дано ВМО ВСВ НОУ с интервальными матричными компонентами в форме:
Закон управления имеет вид:
Система с интервальными матричными компонентами:
Для интервальной
матрицы состояния
Закон
управления изменяет лишь медианную составляющую
На
основе заданных интервальных реализаций параметров
|
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
12 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
Теперь найдем:
Требуемая величина оценки модальной робастности:
Решим матричное уравнение Сильвестра относительно матрицы М:
Сформируем матрицу:
Вычислим оценку относительной интервальности матрицы состояния системы:
Требование выполнено. Получим параметры закона управления:
Закон управления принимает вид:
|
||||||
|
КСУИ.1165147.001 ПЗ |
Лист |
|||||
|
13 |
||||||
|
Изм. |
Лист |
№ докум. |
Подп. |
Дата |
||
|
Заключение. В данной работе были построены модели траекторной чувствительности по всем варьируемым параметрам; параметры были проранжированы по потенциальной чувствительности. Построена модель траекторной чувствительности дискретного |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.