Модель антиблокировочной системы тормозов автомобиля, страница 2

Силы трения функционально зависят от нормальных сил, в которых можно выделить две составляющие. Первая компонента появляется вследствие распределения масс автомобиля, в то время как вторая компонента объясняется переносом масс. Для передних колес первая компонента записывается так:

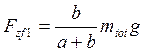, для задних так:

.

Вторая составляющая нормальной силы связана с осевым перемещением веса, вызванным ускорением или торможением. Её можно найти, используя теорему об изменении кинетического момента системы. Рассмотрение моментов относительно точки контакта шины и дороги для переднего колеса дает

, где  является ускорением автомобиля. Поделив обе части на , получим нормальную силу, действующую на переднее колесо,  вызванную переносом веса:

.

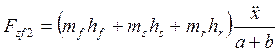Аналогично получаем выражение второй составляющей нормальной силы, действующей на заднее колесо:

.

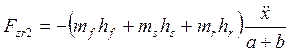Общая нормальная сила, действующая на переднее колесо, есть

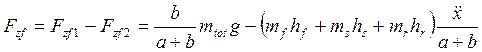, а общая нормальная сила, действующая на заднее колесо, есть

.

Обозначим

,

,

.

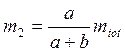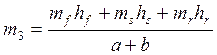Тогда общая нормальная сила, действующая на переднее колесо, может быть выражена следующим образом:

.

А общая нормальная сила, действующая на заднее колесо, получается как

.

Далее определяем суммарную силу трения:

.

Применение второго закона Ньютона относительно оси  дает

.

Объединяя приведенные выше два уравнения, получим формулу

.

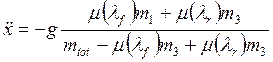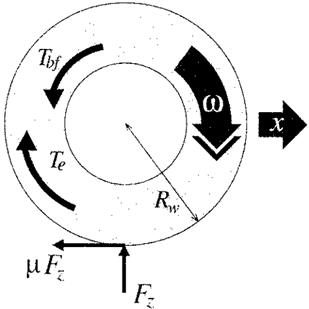
Рис. 4: Диаграмма сил, действующих на переднее колесо

Далее, используя рис. 4, выведем уравнения, моделирующие динамику переднего и заднего колес. Пусть  — крутящий момент, передаваемый от двигателя переднему колесу (предполагаем, что рассматриваемый автомобиль переднеприводный),  — тормозной момент, прикладываемый к переднему колесу,  — тормозной момент, прикладываемый к заднему колесу, и  — радиус колеса. Пусть  обозначает угловую скорость переднего колеса, а  — угловую скорость заднего колеса. Тогда можно получить динамические уравнения для переднего и заднего колес:

,

.

Подставляя (1) и (2) в равенства (4) и (5), получим

,

.

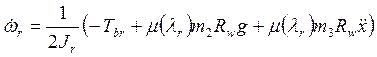Тормозной момент, приложенный к заднему колесу, связан с тормозным моментом, приложенным к переднему колесу, равенством

, где  — коэффициент пропорциональности, выражающий соотношение этих двух моментов. Обычное значение  лежит в диапазоне от 0,2 до 0,6. Таким образом, момент  есть часть момента . Это помогает предотвращать блокировку заднего колеса даже, если блокируется переднее, что обеспечивает определенную маневренность автомобиля.

Из подстановки (8) в (7) находим

.

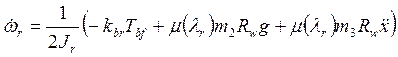Модель тормозной системы автомобиля описывается соотношениями (3), (6), (9). Определим переменные состояния , , , . Используя эти переменные, представим модель тормозной системы автомобиля в форме пространства состояний:

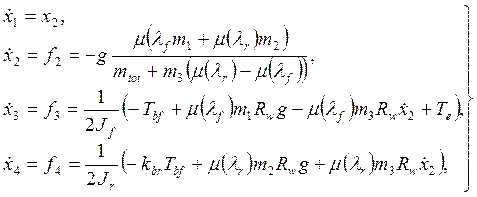
где значения параметров описываются в табл. 1. Выходные значения:

.

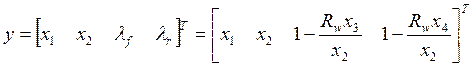Следует заметить, что вышеописанная модель тормозной системы состоит только из четырёх, хотя и нелинейных, дифференциальных уравнений. Тем не менее, она достаточно точно характеризует поведение исследуемой системы.

Моделирование

На основе (10), (11) была составлена Simulink-модель исследуемой системы. Она представлена на рис. 5. В этой модели была использована простейшая схема управления тормозным моментом, основанная на сравнении значения коэффициента проскальзывания для текущего момента времени с его оптимальным значением для данных дорожных условий.

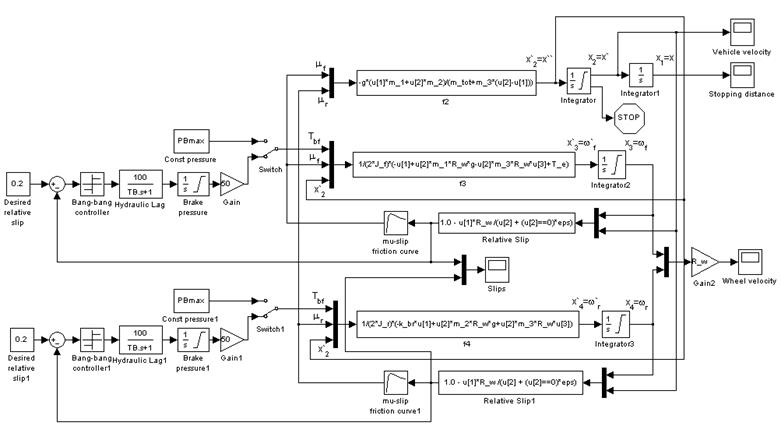
Рис. 5: Simulink-диаграмма модели тормозной системы

На рис. 6, 7, 8 представлены графики  параметров тормозной системы с выключенной АБС.

Рис. 6: Тормозной путь автомобиля, не оборудованного АБС

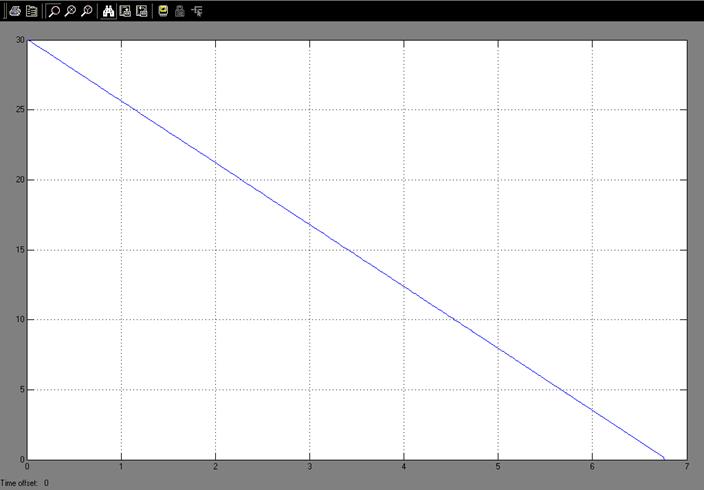
Рис. 7: Скорость автомобиля, не оборудованного АБС

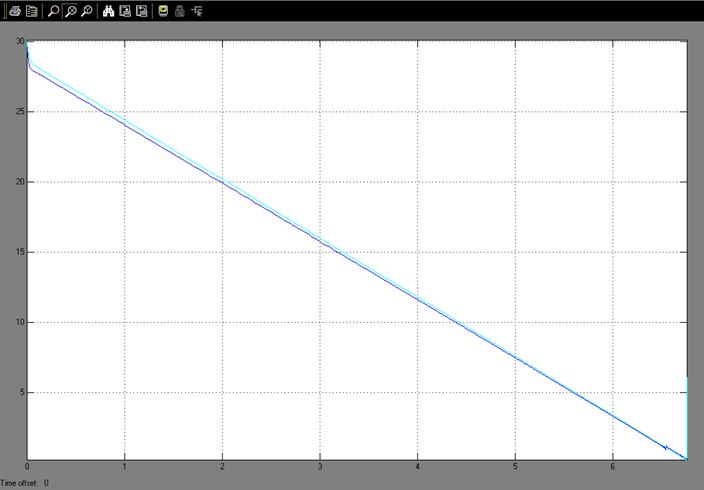
Рис. 8: Скорости колёс передней и задней осей автомобиля, не оборудованного АБС

На рис. 9, 10, 11, 12 представлены графики  параметров тормозной системы с АБС.

Рис. 9: Тормозной путь автомобиля, оборудованного АБС

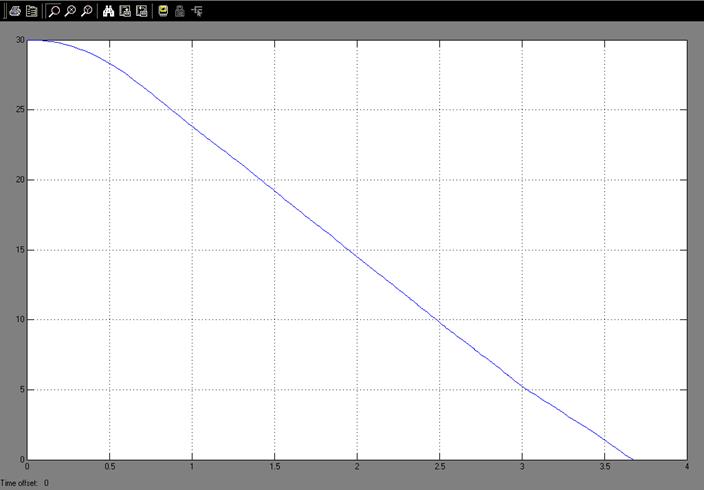
Рис. 10: Скорость автомобиля, оборудованного АБС

Рис. 11: Скорости колёс передней и задней осей автомобиля, оборудованного АБС

Рис. 12: Проскальзывания  и  колёс автомобиля, оборудованного АБС

Из рис. 6–11 видно, что автомобиль, оснащенный АБС, затратил на торможение в 1,5 раза меньше времени по сравнению с автомобилем, не оборудованным АБС. Также примерно в 1.7 раза сократился и тормозной путь.

Заключение. Выводы

Итак, была исследована динамика торможения автомобиля и построена модель этого процесса. Результаты моделирования показывают, что использование даже простейшего закона управления тормозным моментом повышает эффективность торможения — уменьшаются тормозной путь и время торможения, улучшается манёвренность транспортного средства.

Очевидна необходимость разработки более совершенной модели АБС. Для этого нужно спроектировать два дополнительных компонента: контроллер тормозного момента, регулирующий давление в тормозной системе, и блок, оценивающий коэффициент трения между шинами и дорогой. Также требуется получить алгоритм взаимодействия этих двух подсистем.

Библиографическийсписок

·  Yonggon Lee and Stanislaw H. Zak. Designing a genetic neural fuzzy antilock-brake-system controller.

·  Wei-En Ting and Jung-Shan Lin. Nonlinear control design of anti-lock braking systems combined with active suspensions.

·  B. Ewers, J. Bordeneuve-Guibé, Corinne Langlois. A symbolic sensor for an antilock brake system of a commercial aircraft.

·  Jingang Yi, Luis Alvarez, Roberto Horowitz. Adaptive emergency braking control with underestimation of friction coefficient.

·  Mark Denny. The dynamics of antilock brake systems.