Определение отношения удельных теплоемкостей газов.
Цель работы: определить показатель адиабаты (коэффициент Пуассона) методом адиабатного изменения состояния газа (метод Клемана-Дезорма).
Приборы и принадлежности: стеклянный баллон с краном, соединенный резиновой трубкой со стеклянным манометром, насос.
Количество теплоты, необходимое для нагревания единицы массы (одного моля) вещества на один кельвин, называется удельной (молярной) теплоёмкостью вещества. Для газов эти теплоёмкости зависят от условий, при которых происходит нагревание.
Так, удельная и молярная теплоёмкости газов при постоянном давлении больше, чем при постоянном объёме Ср > Сv , так как при нагревании газа при постоянном давлении (изобарический процесс) подведённое к газу количество теплоты идёт на увеличение его внутренней энергии, а следовательно и на увеличение её температуры и на совершение газом работы расширения для поддержания постоянного давления.
Например, если поместить газ в сосуд с подвижным поршнем, обеспечивающим постоянное давление, то, нагревая его, он расширяется и поднимает поршень, совершая таким образом работу против внешних сил. Нагревая газ при постоянном объеме (изохорический процесс) всё количество теплоты, подведённое к газу, идёт на увеличение его внутренней энергии, так как работа газа в этом случае равна нулю.
Коэффициентом Пуассона g называется отношение теплоемкостей при постоянном давлении Ср к теплоемкости при постоянном объеме Сv .
g = (Ср / Сv ) (1)
Метод Клемана - Дезорма для определения коэффициента Пуассона γ основан на адиабатическом расширении или сжатии газа.
Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой.
Коэффициент Пуассона называют также показателем адиабаты, так как он входит в уравнение Пуассона, характеризующее адиабатический процесс:
![]()
Установка для определения γ состоит из стеклянного баллона, соединённого с U – образным водяным манометром и насосом. В пробке баллона укреплён клапан (кран) с пружиной, посредством которого баллон может быть соединён с атмосферой. На шланге, соединяющем баллон с насосом, имеется зажим.
Принцип действия установки состоит в следующем.
В стеклянный баллон накачивается газ до определенного давления р1, превышающее атмосферное:
р1=Н+h1, (2)
где Н- атмосферное давление выраженное в мм водяного столба, h1- разность уровней, т.е. избыток давления сверх атмосферного, измеренный водяным манометром в мм водяного столба.
Температура газа в баллоне увеличится за счёт произведённой работы сжатия. Через некоторое время, вследствие теплообмена через стенки баллона, газ в баллоне примет температуру окружающего воздуха. Быстро открывается клапан (кран) и газ выпускается наружу до тех пор, пока давление в баллоне не станет равным атмосферному давлению.
Выход газа происходит быстро, и, пренебрегая в первом приближении передачей тепла через стенки баллона, процесс расширения газа в баллоне можно считать адиабатическим. При этом расширяющийся газ совершает работу против внешних сил – внешнего атмосферного давления.
Следовательно, температура газа в баллоне понизится.
Если теперь закрыть кран (кран закрывается в тот момент, когда давление в баллоне станет равным атмосферному) и дать газу в баллоне нагреться до температуры окружающей среды, то его давление возрастет до некоторой величины
p2 = H + h2, (3)
где h2 – разность уровней, т.е. избыток давления в баллоне над атмосферным давлением (измеряется в мм водного столба).
Из полученных трех состояний газа в баллоне несложно рассчитать коэффициент Пуассона.
В баллоне выделим мысленно некоторую массу m газа, которая остается в баллоне на протяжении всего эксперимента. Рассмотрим три состояния этой массы, мысленно представляя соответствующие им параметры газа:
|
Состояние системы |
Объем |
Давление |
Температура |
|
Кран закрыт, газ сжат |
V1 |
H + h1 |
Комнатная |
|
Кран открыт, газ адиабатически расширен |
V2 |
H |
Ниже комнатной |
|
Кран закрыт. Температура установилась |
V2 |
H + h2 |
Комнатная |
Сопоставляя первое и третье состояние газа, видим, что температура газа, занимающего объемы V1 и V2 одинакова. Согласно закону Бойля-Мариотта:
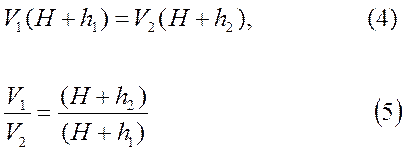
Из 1-го состояния во 2-е произошло адиабатическое расширение, тогда согласно уравнению Пуассона, можно записать
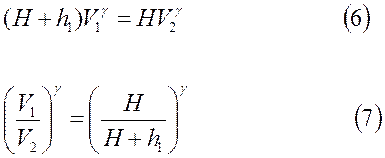
Из этих соотношений следует
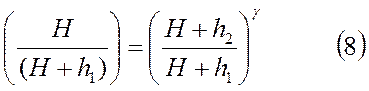
Логарифмирование (8) дает
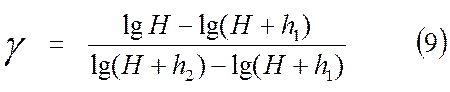
Так как давление H; H + h1 и H + h2 незначительно отличаются друг от друга, то в первом приближении логарифмы величин можно заменить их численными значениями. В таком случае (9) можно записать:
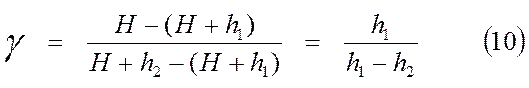 ,
,
т. е. искомая величина
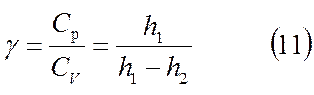 .
.
Задание
Определение отношения Ср/СV для газов

Ход работы.
1.Выбрать газ, над которым будет ставиться эксперимент. 2.Нажать кнопку пуск для начала работы. 3.Измерить разность уровней жидкости в обоих коленах манометра.
4.Нажать кнопку клапан сброса и подождать пока уровень жидкости установится окончательно. 5.Измерить разность уровней жидкости в коленах манометра. 6.Кнопка новый эксперимент запустит эксперимент снова. 7.Повторить опыт не менее 10 раз. 8.Расчитать gпо формуле (2). 9.Оценить погрешность этого метода.
Вопросы.
1. Какая величина измеряется в данной лабораторной работе? 2.Какая величина вычисляется в ходе данной работы? 3.Какие процессы протекают в ходе эксперимента? 4.Против каких внешних сил совершается работа газа? 5.Какой принцип работы данной установки? 6.Каким методом определяется коэффициент Пуассона? 7.Какой процесс называется адиабатическим? 8.Почему молярная и удельная теплоёмкости при постоянном давлении больше чем при постоянном объёме? 9.От чего зависит молярная теплоёмкость газа?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.