Местные гидравлические сопротивления. Внезапное сужение трубопровода. Постепенное расширение трубопровода

Местные гидравлические сопротивления

Потери напора, затраченного на преодоление какого-либо местного сопротивления, оценивается в долях скоростного напора, соответствующего скорости непосредственно за рассматриваемым сопротивлением:

.

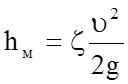Основные виды местных потерь напора можно условно разделить на следующие группы:

а) потери, связанные с изменением сечения потока (внезапное расширение, сужение, а также постепенное расширение и сужение);

б) потери, связанные с изменением направления потока (поворотные колена, угольники, отводы, используемые на трубопроводах);

в) потери, связанные с протеканием жидкости через арматуру различного типа (вентили, краны, обратные клапаны, сетки, отборы и т.д.);

г) потери, связанные с отделением одной части потока от другой или слиянием двух потоков в один общий.

Для понятия основных физических закономерностей рассмотрим потери напора, связанные с изменением сечения потока.

          Внезапное расширение трубопровода

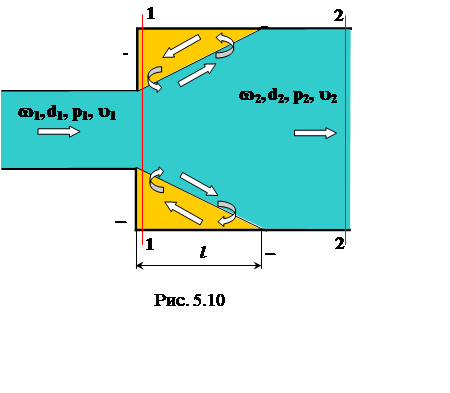          Рассмотрим расширение трубопровода от диаметра d₁ до диаметра d₂ (рис. 5.10).

Экспериментальные исследования позволили установить, что поток, выходящий из узкой струи, не сразу заполняет все поперечное сечение широкой трубы. Жидкость в месте расширения отрывается от стенок и дальше движется в виде свободной струи, отделенной от остальной жидкости поверхностью раздела. Поверхность раздела неустойчива, на ней возникают вихри, в результате чего транзитная струя перемешивается с окружающей жидкостью. Струя постепенно расширяется, и на некотором расстоянии l от начала расширения заполняет все сечение широкой трубы.

Вследствие отрыва потока и связанного с ним вихреобразования на участке трубопровода между сечениями 1 и 2 происходит значительная потеря напора. Давление на торцевой стенке АВ, как показывает опыт, практически равно давлению на выходе из узкой части трубы, т.е. р₁.

Уравнение Бернулли для сечений 1 и 2, принимая a₁ = a₂ » 1, запишется в виде:

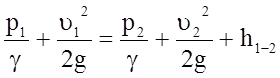,                                           (5.76)

откуда

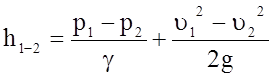.                                            (5.77)

Из теоремы импульсов для сечений 1 и 2, пренебрегая силами трения, можно получить:

(р₁ - р₂)w₂ = Qr(u₂ - u₁).

Разделив обе части этого уравнения на g, получим:

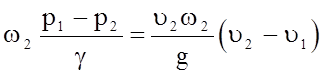
или 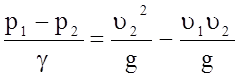    .                                        (5.78)

Подставляя полученное выражение в уравнение (5.77) получаем:

.

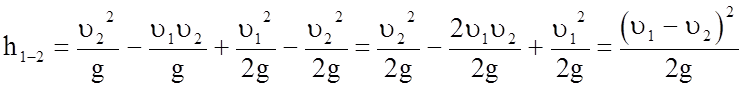Из этого выражения следует, что потери напора при внезапном расширении равны скоростному напору от потерянной скорости. Данное уравнение носит название формулы Борда, которую можно привести к виду

.

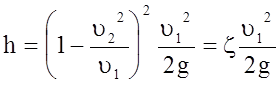Таким образом, величина z определяется, как

.

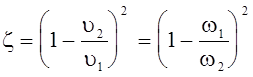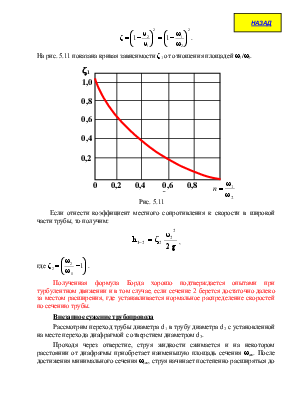
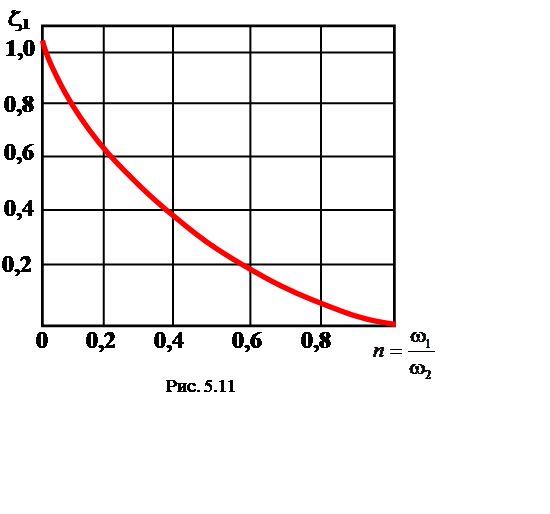
На рис. 5.11 показана кривая зависимости z₁ от отношения площадей w₁/w₂.

Если отнести коэффициент местного сопротивления к скорости в широкой части трубы, то получим:

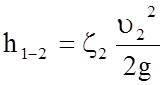, где .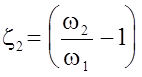

Полученная формула Борда хорошо подтверждается опытами при турбулентном движении и в том случае, если сечение 2 берется достаточно далеко за местом расширения, где устанавливается нормальное распределение скоростей по сечению трубы.

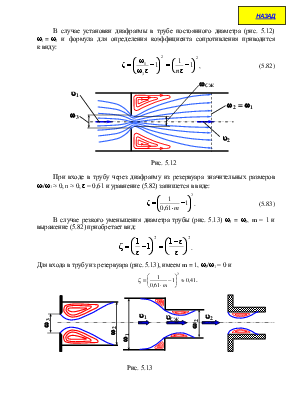
          Внезапное сужение трубопровода

Рассмотрим переход трубы диаметра d₁ в трубу диаметра d₂ с установленной на месте перехода диафрагмой с отверстием диаметром d₃.

Проходя через отверстие, струя жидкости сжимается и на некотором расстоянии от диафрагмы приобретает наименьшую площадь сечения