Давление жидкости на твердые поверхности

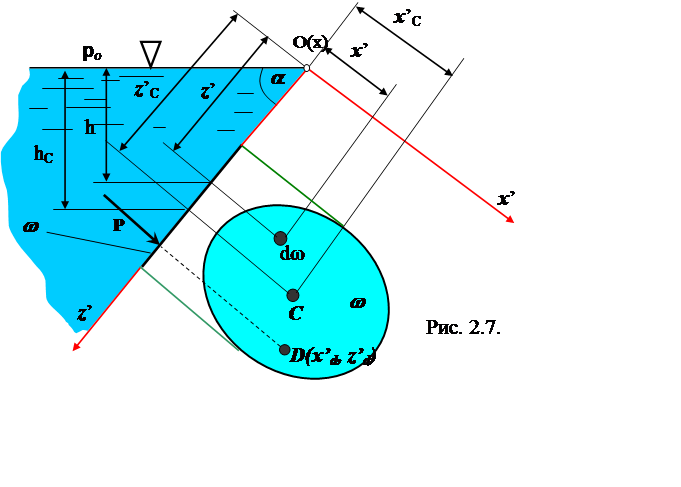
Давление жидкости на твердые поверхности

Давление жидкости на плоские стенки

Рассмотрим давление жидкости на плоскую стенку, которая наклонена к горизонту под углом a. Определим силу Р, действующую на площадку w (рис. 2.7).

Величину силы Р, действующей по нормали к площадке, можно определить, как

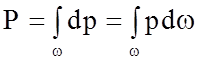.                       (2.53)

Принимая во внимание, что

р = р₀ + gh

имеем 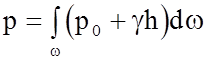                                    .                                         (2.54)

Направим ось Ох по линии пересечения свободной поверхности воды с плотностью стенки и перпендикулярно координатной оси Оz¢, которая направлена вниз вдоль стенки.

В этой системе координат  .

Тогда,

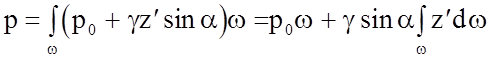.            (2.55)

Известно, что статический момент площади относительно любой оси  равен произведению этой площади на расстояние от центра ее тяжести до оси моментов.

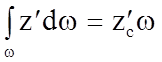,                                             (2.56)

где z¢_c - расстояние от центра тяжести С площадки w до оси Ох¢ (оси моментов)

Делая соответствующие подстановки, имеем

P = p₀w + g sina z¢_cw = p₀w + gh_cw                                 (2.57)

или, за вычетом атмосферного давления

P = gh_cw.                                                  (2.58)

Таким образом, сила, с которой жидкость действует на плоскую стенку, равна весу жидкости в объеме цилиндра с основанием, равным площади данной стенки, и высотой, равной глубине погружения центра тяжести этой площадки под уровень свободной поверхности.

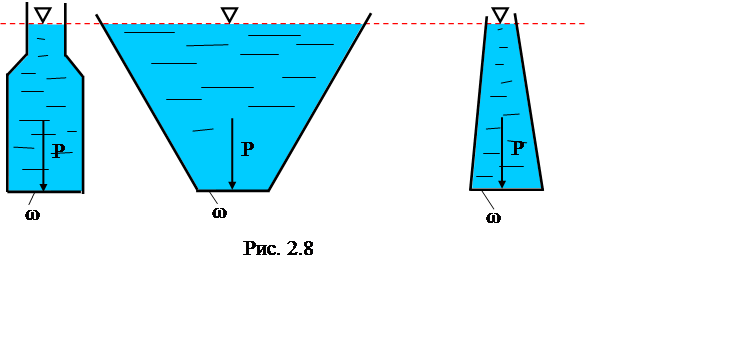
Необходимо отметить, что для различных по форме резервуаров (рис. 2.8), имеющих одинаковую площадь основания, давление на дно будет одинаковым во всех случаях.

Точка приложения D силы давления на плоскую стенку будем определять исходя из следующих соображений: точка D лежит в плоскости стенки. Для определения ее координат воспользуемся теоремой Вариньона, согласно которой момент равнодействующей системы параллельных сил равен сумме моментов сил ее составляющих.

m (P)_ox = S m(dP)_ox .                                       (2.59)

Момент силы P равен:

m (P)_ox = Pz_d².                                                 (2.60)

Момент элементарной силы dP равен:

m (dP)_ox = z¢dP.                                                (2.61)

С учетом этого уравнение моментов запишется в виде:

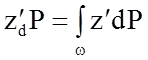.                                                  (2.62)

Величины сил P и dP можно определить, как

P = gh_cw = gz_c¢sin a × w;                                          (2.63)

dP = gz_c¢sin a × dw.                                          (2.64)

Подставляя записанные выражения в уравнения моментов? и решая его относительно z¢d, имеем

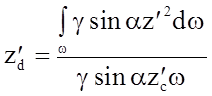                                         (2.65)

или, сокращая числитель и знаменатель на g×sina,

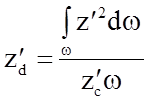.                                            (2.66)

Здесь числитель представляет собой момент инерции площади w относительно координатной оси Ох:

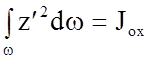,                                        (2.67)

а по теореме о моментах инерции относительно параллельных осей можем написать

J_ox = J_o + z_e¢²w,                                       (2.68)

где J_o - момент инерции площади w относительно оси, проходящей через центр тяжести площади w и параллельной оси Ох.

Тогда, имеем

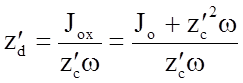                                   (2.69)

или 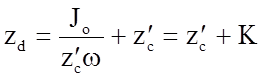     .                           (2.70)

Величина К имеет размерность длины и иногда называется эксцентриситетом. Величина К положительна и, следовательно, центр давления (точка D) лежит на большей глубине, чем центр тяжести (точка C) данной площади w (z¢_d > z¢_c).

Рассмотрим давление жидкости на непроницаемую криволинейную поверхность (рис. 2.9).

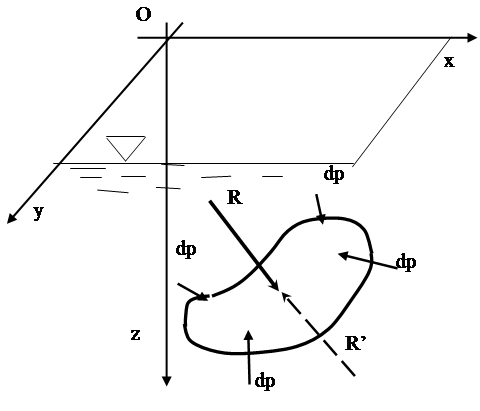Так как поверхность пластинки криволинейна, то силы dp образуют систему непараллельных сил. Такая система в общем случае приводится к главному вектору и одной паре сил. Разложим каждую элементарную силу dP на три составляющие по координатным осям.

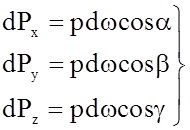,                                    (2.71)

где a, b и g - углы наклона элементарных сил dP к координатным осям, различные для разных площадок dw.

Суммируя проекции элементарных сил, найдем соответствующие проекции равнодействующей силы R:

R_x = S pdw cos a;                                          (2.72)

R_y = S pdw cos b;                                           (2.73)

R_z = S pdw cos g .                                           (2.74)

Силу R можем определить следующим образом:

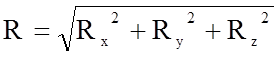,                           (2.75)

а направление линии ее действия найдем по направляющим косинусам

cosa = R_x/R;                                             (2.76)

cosb = R_y/R;                                             (2.77)

cosg = R_z/R.                                              (2.78)

Величины проекций элементарной силы dR запишутся в виде

dR_x =  pdw cos a = pdw_x;                                                                 (2.79)

dR_y =  pdw cos b = pdw_y ;                                           (2.80)

dR_z =  pdw cos g = pdw_z,.                                            (2.81)

где dw_x,  dw_y,  dw_z - проекции площадки dw на плоскости, перпендикулярные осям Ох, Оy, Oz.

Интегрируя, записанные выше выражения, получаем

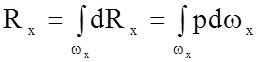.                                  (2.82)

Записанный интеграл представляет собой силу давления жидкости на всю плоскую площадку w_х, поэтому

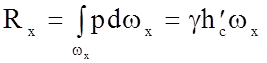,                                  (2.83)

где h_с¢ - глубина погружения центра тяжести площади w_х под уровень свободной поверхности.

По аналогии

R_y = gh_c²w_y.                                               (2.84)

Вертикальная проекция силы R определится, как

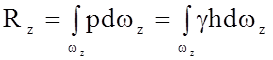,                                (2.85)

где h - глубина погружения площадки dw_z под уровень свободной поверхности.

Произведение hdw_z можно рассматривать как элементарный объем