Источники и стоки. Определение потенциала скорости и функции тока для источника

Источники и стоки.

Источником называется точка (а в случае плоскопараллельного течения - прямая), из которой непрерывно и равномерно вытекает жидкость по радиальным прямым.

Стоком называется точка (прямая), к которой наоборот, стекает жидкость.

Определим потенциал скорости j и функцию тока y для источника. Непосредственно из определения очевидно, что линии тока будут радиальными прямыми, а в таком случае линии равного потенциала скорости должны быть окружностями (рис. 3.13).

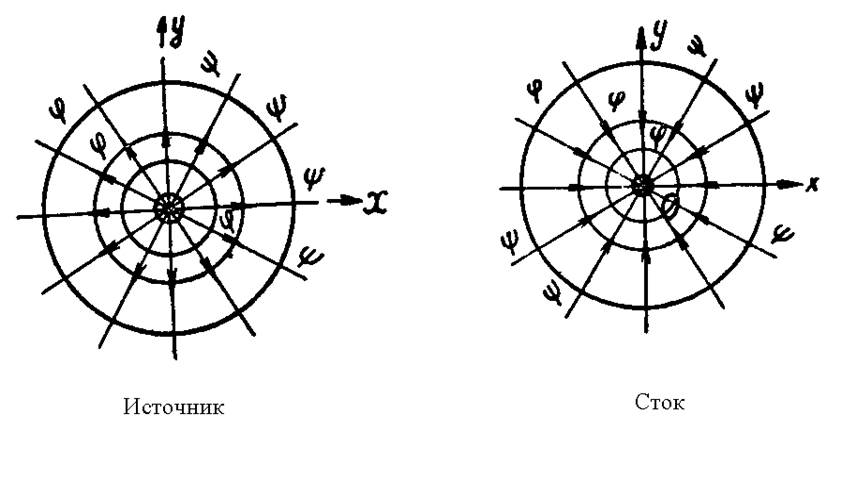
Уравнением функций тока является y = с·a, где a - угол, образуемый данной радиальной прямой с осью Ох. Учитывая, что a = arctg (y/x), имеем:

y = с·arctg (y/x).                                            (3.111)

Скорость V любой частицы жидкости на расстоянии r от центра определится, как

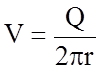,                                                (3.112)

где Q - расход жидкости на единицу длины.

          Проекции скорости V определятся, как

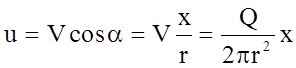;                                  (3.113)

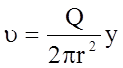.                                             (3.114)

Подставляя их значения в значения дифференциала потенциала скорости, имеем

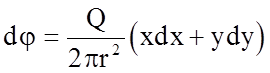,                               (3.115)

но учитывая, что

xdx + ydy = rdr                                             (3.116)

получаем:

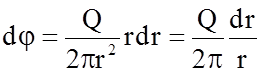.                               (3.117)

Интегрируя уравнение (3.117), получаем:

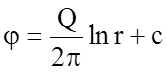    .                                        (3.118)

Полагая с = 0, имеем:

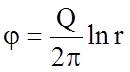                                            (3.119)

или

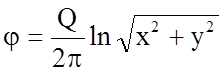.                                     (3.120)