


 Основное
дифференциальное уравнение гидростатики
Основное
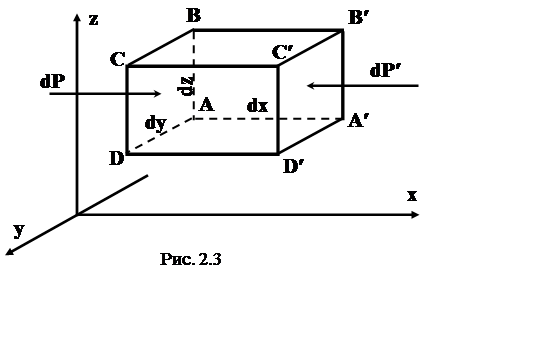
дифференциальное уравнение гидростатикиРассмотрим внутри покоящейся жидкости параллелепипед с ребрами (рис. 2.3), расположенными параллельно координатным осям Оx, Oy, Oz и равными соответственно dx, dy, dz. Принимая во внимание, что уравнения моментов не имеют смысла, рассмотрим уравнение равновесия сил в проекциях на координатные оси.
å Х = 0; å Y = 0; å Z = 0. (2.12)
Для оси Ох имеем
dP - dP1 + dFcosa = 0, (2.13)
где dP = pdydz и dP1 = p¢dydz;
P1 и P¢ - средние гидростатические давления соответственно на площадки АВСДА и А¢В¢С¢Д¢А¢.
Принимая во внимание, что гидростатическое давление является функцией координат, среднее гидростатическое давление на площадке А¢В¢С¢Д¢А¢ будет равно
p¢ = 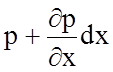 .
.![]() (2.14)
(2.14)
 |
Тогда, силу dP1 можно определить, как
![]()
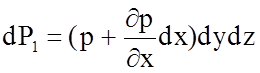 .
(2.15)
.
(2.15)
Объемная сила для массы dm, заключенной в объеме параллелепипеда, определится как
dF = dmjcosa = dmX = rdxdydzX. (2.16)
 Подставляя
значения слагаемых, получаем:
Подставляя
значения слагаемых, получаем:
 pdydz-
pdydz- 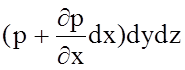
![]() + rXdxdydz =
0. (2.17)
+ rXdxdydz =
0. (2.17)
Проводя преобразования (раскрывая скобки и сокращая на dxdydz ) получаем
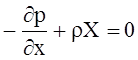 .
(2.18)
.
(2.18)
Аналогично получаются и уравнения проекций сил на оси Oy и Ox.
Тогда, систему уравнений описывающих условия равновесия жидкости (уравнение Эйлера) можно записать в виде
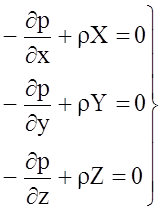 .
(2.19)
.
(2.19)
Запишем уравнение Эйлера в виде
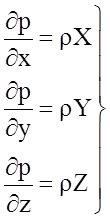 .
(2.20)
.
(2.20)
Умножая каждое из записанных уравнений на dx,dy и dz соответственно, и проводя сложение правых и левых частей уравнений, получим
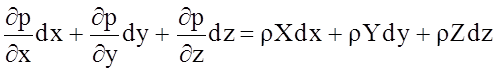 . (2.21)
. (2.21)
Принимая во внимание, что левая часть записанного уравнения представляет собой полный дифференциал dp функции p = p(x, y, z), имеем
dp = r (Xdx + Ydy + Zdz). (2.22)
Данное уравнение называется основным дифференциальным уравнением гидростатики.
Логично предположить, что правая часть уравнения представляет также полный дифференциал некоторой функции
 Xdx + Ydy +Zdz = dU.
(2.23)
Xdx + Ydy +Zdz = dU.
(2.23)
Следовательно, X = ¶U/¶x; Y = ¶U/¶y; Z = ¶U/¶z.
Величины x, y, z представляют собой проекции ускорения объемной силы, которые можно рассматривать как проекций самой объемной силы, отнесенной к единице массы данной жидкости.
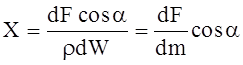 ; (2.24)
; (2.24)
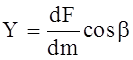 ;
(2.25)
;
(2.25)
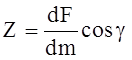 .
(2.26)
.
(2.26)
Функция U (x, y, z) является потенциалом сил или так называемой “силовой функцией”.
Таким образом, равновесие жидкости возможно, если объемные силы имеют потенциал.
Для поверхностей уровня наблюдается равенство давлений во всех точках - p = const и dp = 0.
Тогда, основное уравнение гидродинамики запишется в виде
Xdx + Ydy + Zdz = 0. (2.27)
Основные свойства поверхностей уровня:
1. Две поверхности уровня не пересекаются между собой.
 2. Внешние объемные силы направлены нормально к поверхности
уровня.
2. Внешние объемные силы направлены нормально к поверхности
уровня.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.