
































Токи в остальных ветвях исходной схемы определяют, пользуясь законами Кирхгофа и Ома.
АНАЛИЗ И РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С НЕСКОЛЬКИМИ ИСТОЧНИКАМИ ПИТАНИЯ
1. Законы Кирхгофа. Расчет любой электрической цепи можно провести, используя законы Кирхгофа.
Первый закон Кирхгофа ![]()
![]() ;
;
второй закон Кирхгофа ![]() .
.
Уравнения составляются в следующем порядке. Определяют число ветвей (в) и узлов (у) в электрической цепи. Общее количество уравнений, которое необходимо составить, равно количеству неизвестных токов (количеству ветвей). По первому закону Кирхгофа составляют (у-1) независимых уравнений. Остальные уравнения составляют по второму закону Кирхгофа (в-у+1). Например, схема, показанная на рис. 4, имеет 6 ветвей и 4 узла, поэтому по первому закону Кирхгофа необходимо составить 3 уравнения (4-1) и 3 уравнения по второму закону Кирхгофа, так как число неизвестных токов равно числу ветвей.
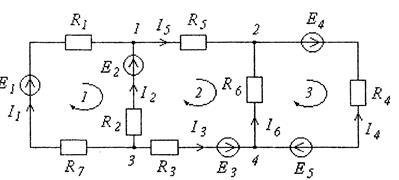 Для записи уравнений
необходимо выбрать (произвольно) положительные направления токов в ветвях и
направления обхода контуров. В уравнении, составляемом по первому закону рис.1.
Кирхгофа, токи, направленные
от узла, записываются со знаком плюс, направленные к
узлу, - со знаком минус. Для 1 узла схемы цепи на рис. 4 уравнение имеет вид:
-I1-I2+I5=0. При
составлении уравнений по второму закону Кирхгофа со знаком плюс записываются те
слагаемые, в которых ток и ЭДС имеют направления, совпадающие с направлением
обхода контура. Например, для контура 2 уравнение имеет вид: R2I2-R3I3+R5I5-R6I6=E2-E3. Решая
систему уравнений, составленную по законам Кирхгофа, можно определить токи во
всех ветвях схемы заданной цепи. Если в результате решения системы уравнений
получаются отрицательные значения токов, то это означает, что истинные
направления этих токов противоположны выбранным при составлении уравнений.
Для записи уравнений
необходимо выбрать (произвольно) положительные направления токов в ветвях и
направления обхода контуров. В уравнении, составляемом по первому закону рис.1.
Кирхгофа, токи, направленные
от узла, записываются со знаком плюс, направленные к
узлу, - со знаком минус. Для 1 узла схемы цепи на рис. 4 уравнение имеет вид:
-I1-I2+I5=0. При
составлении уравнений по второму закону Кирхгофа со знаком плюс записываются те
слагаемые, в которых ток и ЭДС имеют направления, совпадающие с направлением
обхода контура. Например, для контура 2 уравнение имеет вид: R2I2-R3I3+R5I5-R6I6=E2-E3. Решая
систему уравнений, составленную по законам Кирхгофа, можно определить токи во
всех ветвях схемы заданной цепи. Если в результате решения системы уравнений
получаются отрицательные значения токов, то это означает, что истинные
направления этих токов противоположны выбранным при составлении уравнений.
2. Метод контурных токов. Сущность метода состоит в уменьшении числа совместно решаемых уравнений путем замены реальных токов ветвей расчетными контурными токами. Благодаря этому число достаточных для расчета уравнений равно (в-у+1) - количеству независимых контуров схемы электрической цепи. Расчет ведется следующим образом. Выделяем необходимое число контуров, в каждом из которых протекает контурный ток. Произвольно задаемся направлением контурных токов; целесообразно все токи направить в одном направлении (на рис. 5 контурные токи Jк направлены по часовой стрелке).
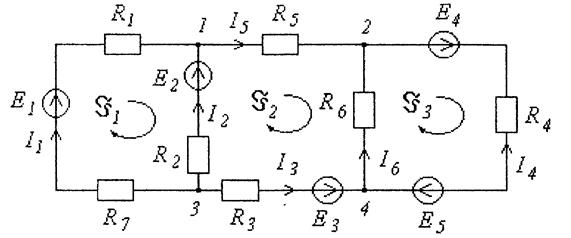 рис.
5.
рис.
5.
Составляем для каждого контура уравнение по второму закону Кирхгофа. При этом направление обхода контуров выбираем совпадающим с направлением контурного тока. Для рассматриваемой схемы система уравнений имеет вид :
(R1+R2+R7) J1-R2J2=E1-E2;
-R2 J1+(R2+R3+R5+R6)J2-R6J3=E2-E3;
-R6J2+( R4+R6)J3=E4+E5.
Так как направление обхода контура совпадает с направлением тока в этом контуре, то падение напряжения от этого тока записано со знаком плюс. В общих ветвях токи смежных контуров направлены противоположно току контура, поэтому падение напряжения от токов смежных контуров записано со знаком минус. Решая систему уравнений, находят контурные токи. Токи в ветвях схемы определяются как алгебраическая сумма контурных токов, протекающих через ветвь. Если направление контурного тока совпадает с направлением тока ветви, то он берется со знаком плюс, если не совпадает, - со знаком минус. Так: I1=J1;I2= -J1+J2; I3= -J2;
I4= -J3; I5=J2; I6= -J2+J2;
 3. Метод междуузлового
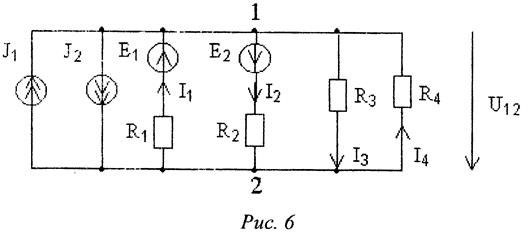
напряжения. В реальных электрических цепях часто несколько источников и
приемников электрической энергии включаются параллельно. Схема замещения такой
цепи, содержащей активные и пассивные ветви, соединенные параллельно, имеет
только два узла (узлы 1 и 2, в схеме на рис. 6).
3. Метод междуузлового
напряжения. В реальных электрических цепях часто несколько источников и
приемников электрической энергии включаются параллельно. Схема замещения такой
цепи, содержащей активные и пассивные ветви, соединенные параллельно, имеет
только два узла (узлы 1 и 2, в схеме на рис. 6).
Если схема содержит k источников тока и m источников ЭДС, то напряжение U12 между узлами:
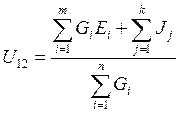
Произведения GiЕi и Jj берутся со знаком плюс, когда Еi и Jj направлены к узлу, потенциал которого условно принят за более положительный (к узлу с первым индексом). Напряжение U12 в электрической схеме, показанной на рис. 6, рассчитывается по формуле:
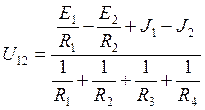
Определив величину напряжения на параллельных ветвях, можно рассчитать токи в ветвях схемы по закону Ома для актив¬ной и пассивной ветвей:
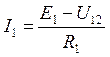 ,
,
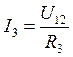 ,
,
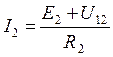 ,
,
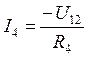
4. Метод эквивалентного активного двухполюсника. Если при анализе сложных электрических цепей нас интересует состояние только
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.