Определение величины силы гидростатического давления на клапан водовыпуска. Определение напора, который необходимо поддерживать на насосе, установленном на пожарный гидрант

2. Практическая часть

          Задача 5. Определить величину силы гидростатического давления Р на клапан водовыпуска АВ диаметром d=2.5 м и точку приложения ее результирующей силы yцо (hцо), если угол наклона боковой стенки пожарного водоема α=60°, а глубина погружения точки A равна H=1.5 м. Построить эпюру давления на затвор и решить задачу аналитическим и графоаналитическим методами.

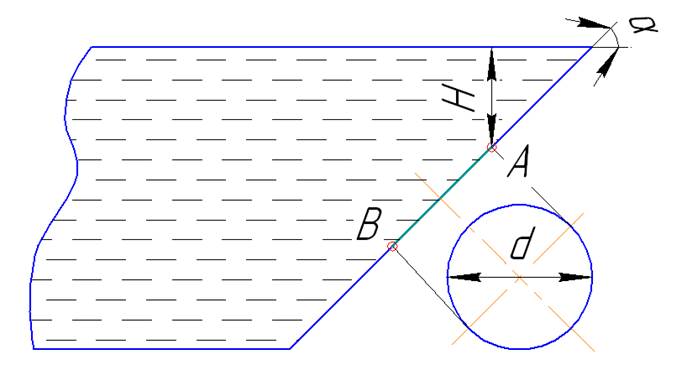
Рисунок 2.1

Дано: d=2.5 м, α=60°, H=1.5 м. Найти: P-?, yцо(hцо)-?

Решение:

Строим эпюру распределения давления по высоте клапана, для чего находим значения давления в точках А и В:

Эпюра распределения давления показана на рисунке 2.2

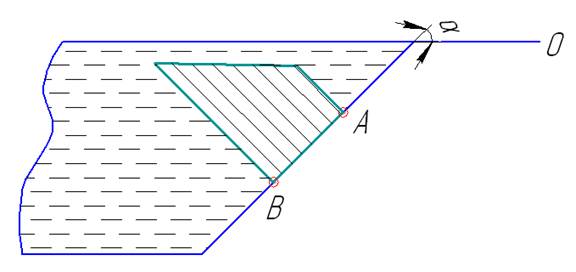
Рисунок 2.2

Аналитический метод:

Результирующая сил давления, воспринимаемая стенкой:

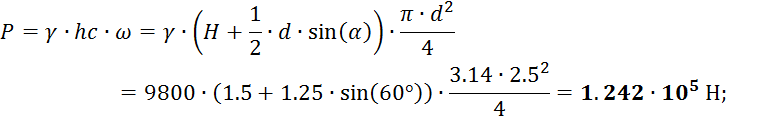
Положение центра давления в плоскости стенки:

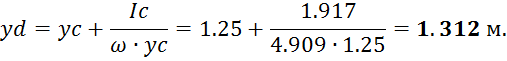
Или    

Результирующая сила и точка ее приложения показаны на рисунке 2.3

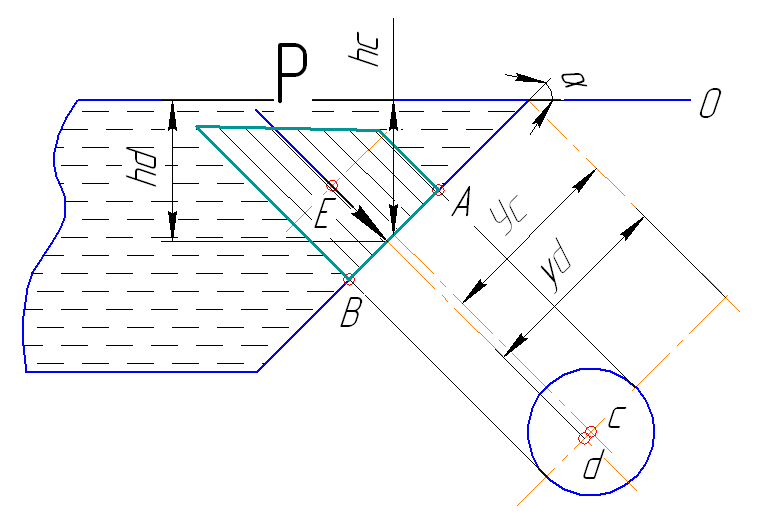
Рисунок 2.3

Графоаналитический метод:

Результирующая сила определяется как объем эпюры распределения нагрузки:

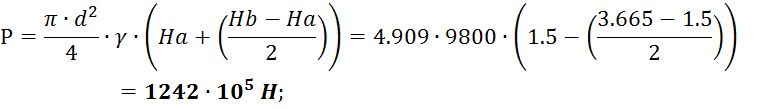
Сила проходит через центр тяжести эпюры распределения нагрузки Е (Рисунок 2.3), тогда, из рисунка yd=1.31 м, hd=2.97 м.

Задача 12.  Определить длину трубы, при которой расход воды из бака (Рисунок 2.4) будет в два раза меньше, чем из отверстия того же диаметра d=60 мм. Напор над центром отверстия равен H=8 м. Коэффициент гидравлического трения в трубе принять λ=0.025, коэффициент расхода отверстия μ=0.62 . Потери напора на входе в трубу и выходе из нее не учитывать.

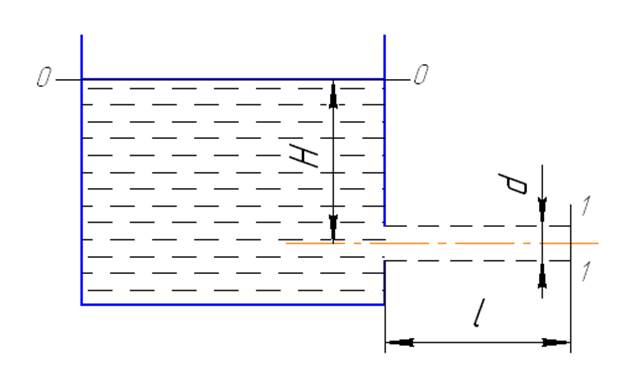
Рисунок 2.4

Дано: H=8 м, d=60 мм; λ=0.025; μ=0,62. Найти: l-?

Решение

1.  Расход воды через отверстие:

2.  Уравнение Бернулли для 0-1:

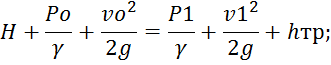
Потери в трубопроводе hтр определим по формуле Дарси-Вейсбаха, учитывая, что Po=P1=0, vтр=v1 vo=0, получим:

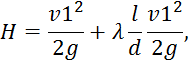
Откуда:

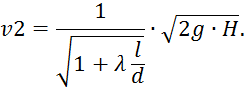
Расход воды через трубу:

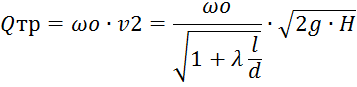
3.  По условию задачи имеем:

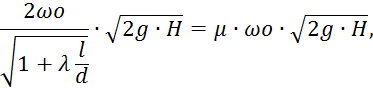
Откуда длина отверстия:

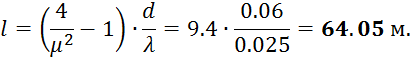
Задача 14. Поршень диаметром D=60 мм движется равномерно вниз в цилиндре, подавая воду в открытый резервуар с постоянным уровнем (Рисунок 2.5). Диаметр трубопровода d=20 мм, его длина l=6 м. Когда поршень находится ниже уровня на H=5 м, необходимая для его перемещения сила равна F=1370 H. Определить скорость поршня и расход воды в трубопроводе. Коэффициенты сопротивления входа в трубу и выхода из нее  ζвх=0.5, ζвых=1.0. Коэффициент гидравлического трения трубы принять равным λ=0.03.

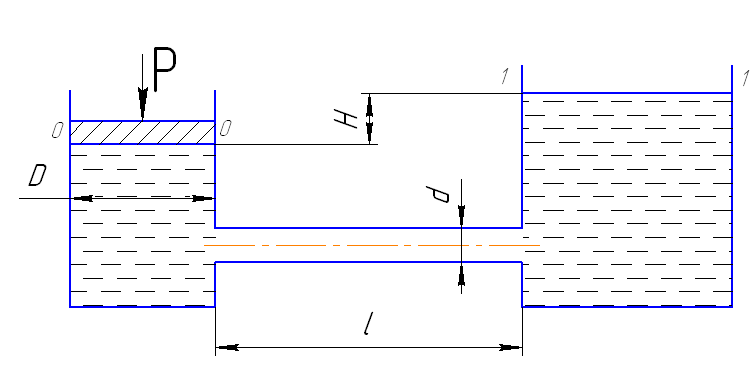
Рисунок 2.5

Дано: H=5 м, D=60 мм; d=20 мм; λ=0.03; F=1370 Н; ζвх=0.5, ζвых=1.0  . Найти: Vп, Qтр-?

Решение:

1.  Составим уравнение Бернулли для сечений 0-1:

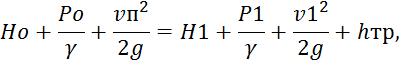
где     Но=0, Po=F/ωп, γ=ρg, P1=0, v1=0. Потери в трубопроводе:

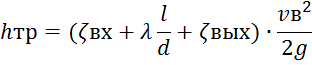
Согласно теории подобия будем иметь:

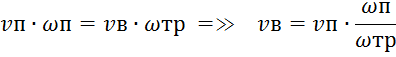
Тогда:

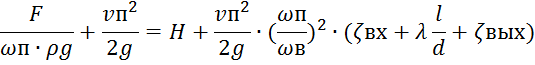
Скорость движения поршня:

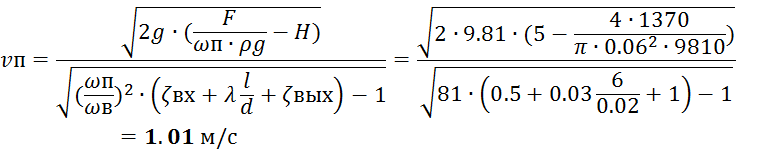
2.  Расход воды в трубе:

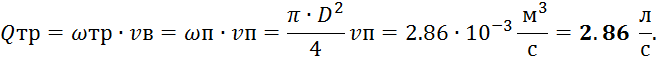
Задача 17. Определить расход Qc, который можно получить в точке C  трубопровода, показанного на рисунке 2.6, если диаметр и длина отдельных участков составляют: d1=175 мм, d2=200 мм, d3=250 мм, l1=150 м, l2=170 м, l3=200 м. Напор в точке A равен Hа=40 м, а геодезические точки – Za=0, Zc=10 м (трубы стальные).

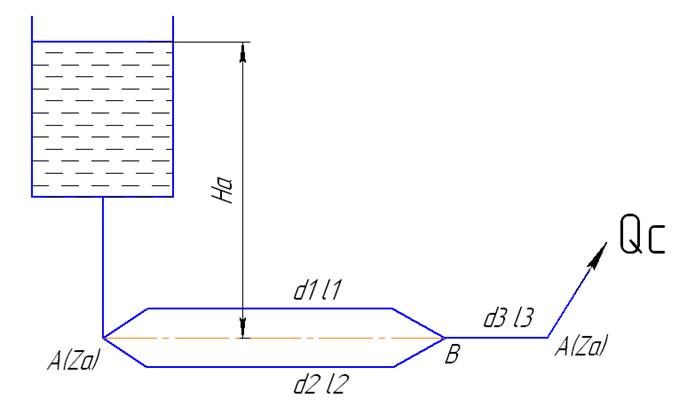
Рисунок 2.6

Дано: d1=175 мм, d2=200 мм, d3=250 мм, l1=150 м, l2=170 м, l3=200 м, Hа=40 м, Za=0, Zc=10 м. Найти: Qc-?

Решение:

Напор в точке A расходуется на преодоление сопротивлений и подъем воды:

По сокращенной формуле Дарси-Вейсбаха потери напора:

где Sобщ – общее сопротивление трубопроводов. Для параллельно соединенных трубопроводов:

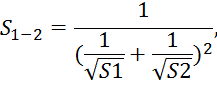
для последовательно соединенных:

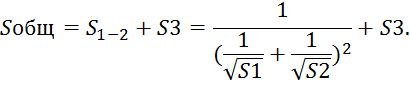
Определяем сопротивления трубопроводов:

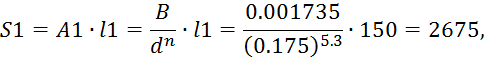
где, для стальных водопроводных труб, В=0.001735, n=5.3 .

Аналогично:

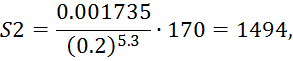
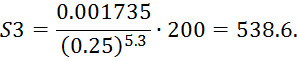
Общее сопротивление трубопроводов:

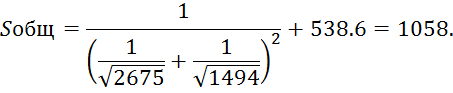
Расход в точке С:

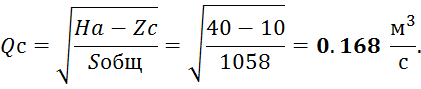
Задача 21. Определить расход воды через систему, состоящую из двух резервуаров и трубопровода переменного сечения диаметрами d1=200 мм, d2=125 мм и длиной l1=105 м, l2=60 м (рисунок 2.7). Разность уровней в резервуарах постоянная и равна H=6.2 м. Эквивалентная шероховатость стенок трубы ∆=0.085 мм. Коэффициенты сопротивления сужения ζсуж=0.18, задвижки ζз=4.5 входа ζвх=0.5, выхода ζвых=1.

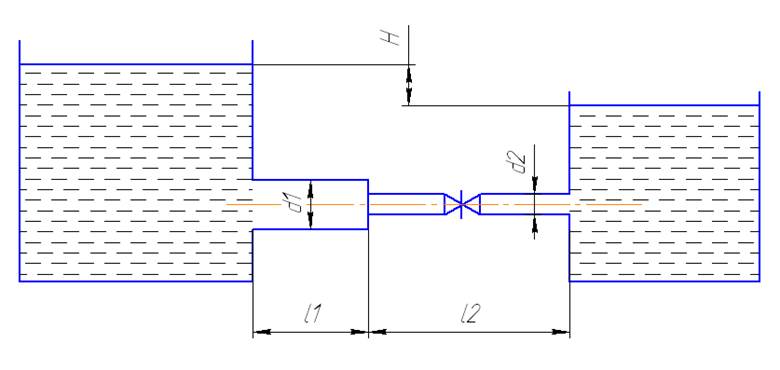
Рисунок 2.7

Дано: H=6.2 м, d1=200 мм, d2=125 мм, l1=105 м, l2=60 м, ∆=0.085 мм,  ζсуж=0.18, ζз=4.5, ζвх=0.5, вых=1. Найти: Qсист-?

Решение:

Потери напора H обусловлены потерями в трубопроводах:

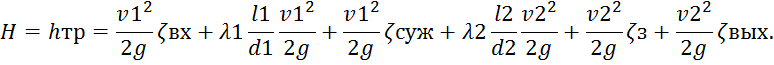
Воспользовавшись теоремой подобия, получим:

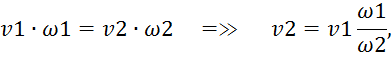
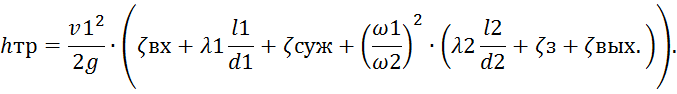
Таким образом:

где

Значения λ1 и λ2 получаем по формуле Шифринсона:

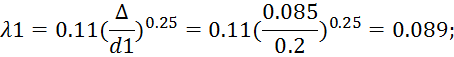
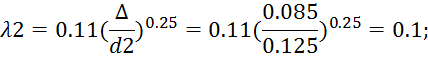
Расход через систему:

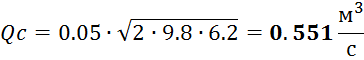
Задача 26.  Определить необходимую толщину стенок прорезиненных рукавов диаметром d=89 мм, чтобы напряжение в них при мгновенном перекрытии  не превышало  . Начальное давление  , количество рукавов n=5, расход воды Q=0.01 м³/с. Скорость распространения ударной волны принять c=100 м/с.

Дано: [σ]= ,  , Q=0.01 м³/с,  d=89 мм, c=100 м/с, n=5. Найти: δ-?

Решение:

Давление после перекрытия:

увеличение давления ∆P определяется по формуле Жуковского:

.

Скорость движения воды в пожарных рукавах:

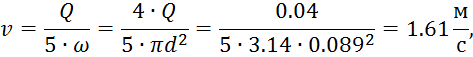
Из условия прочности:

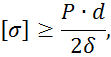
определяем толщину стенок:

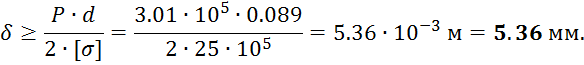
Для 20-и метрового рукава фаза удара составит:

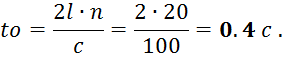
Задача 28. Определить производительность ствола Q с насадком d_н=28 мм при напоре перед ним Н_н=50 м. Построить в масштабе огибающую кривую раздробленной части R_р, в зависимости от угла наклона радиуса действия струи к горизонту. Вычислить величину реакции струи.

Дано: d_н=28 мм, Н_н=50 м. Найти: Q, Rp=f(θ), F-?.

Решение:

Расход жидкости из пожарных стволов определим по формуле

Высоту вертикальной струи определим по формуле Люгера:

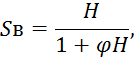
где       φ – коэффициент для различных диаметрах насадков, при dн=28 мм принимаем φ=0.005 .

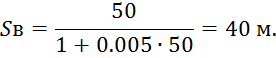
Величину компактной струи определим как часть всей вертикальной струи:

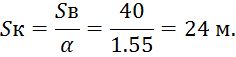
Величина радиуса действия раздробленной струи:

где β – коэффициент, зависящий от угла наклона θ’.

Данные для построения огибающей кривой раздробленной части струи приведены в таблице 2.1. Огибающая кривая показана на рисунке 2.8 .