Зависимость шероховатости поверхности детали от режимов резания, страница 4

                                                                      

 дисперсия среднего арифметического в каждой строке таблицы:

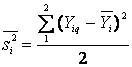, (2)

где i – номер строки;

q=1, 2 – номер параллельного опыта.

По максимальной дисперсии опытов  и сумме дисперсий всех опытов  вычисляют значение

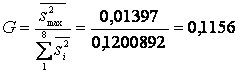, (3)

которое не превышает G_табл=0,516.

2.  Подсчитывается дисперсия воспроизводимости опытов:

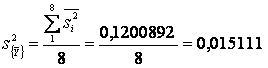. (4)

3.  Определяются неизвестные коэффициенты полинома (1):

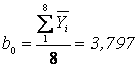, (5)

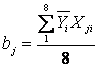, (6)

где j – номер столбца в таблице 1,

X_ji – кодированное значение фактора в соответствующем столбце таблицы 1 (+1 или -1)

b₁= -0,31874;

b₂= 0,102533;

b₃= 0,122864.

Оценивается их статистическая значимость:

, (7)

где t=2,12 – коэффициент Стьюдента.

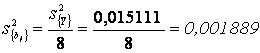, (8);

,

Δb_j= 0,092139< |b_j|. (9)

Выполнение условия (9) подтверждает значимое влияние оцениваемого фактора X_j на выходной параметр Y.

4.  Записав выражение полинома (1) с известными коэффициентами b₀ и b_j для каждой строки таблицы 1 с кодированными факторами (+1,-1), определяют расчетные значения выходного параметра Y_i и записывают в таблицу 3. С этими значениями сравниваются значения Y_i из таблицы 2.

Таблица 3

Номер строки		Ŷi	ΔYi=- Ŷi
1	3,786	3,890	-0,104	0,011
2	3,276	3,253	0,023	0,001
3	4,115	4,095	0,020	0,000
4	3,519	3,458	0,062	0,004
5	4,212	4,136	0,076	0,006
6	3,504	3,498	0,006	0,000
7	4,350	4,341	0,009	0,000
8	3,613	3,703	-0,090	0,008