Цепи согласования, простая схема на выходе. Расчёт критического режима АЭ при гармоническом напряжении на выходе

ЛЕКЦИЯ 4.

4.1. ЦЕПИ СОГЛАСОВАНИЯ. ПРОСТАЯ СХЕМА НА ВЫХОДЕ.

Назначение цепей согласования состоит в том, чтобы согласовать выходное сопротивление активного элемента с нагрузкой и фильтровать высшие (ненужные) гармоники.

Изобразим схему выходной цепи ГВВ в следующем виде:

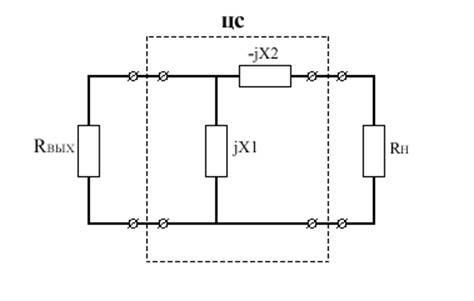
Рис.1

Rвых – выходное сопротивление активного элемента ГВВ

Х1,Х2 – реактивное сопротивление цепи согласования. В простейшем случае это ёмкость и индуктивность колебательного контура;

Rн – сопротивление полезной нагрузки. Для лампового ГВВ  Rн<< Rвых. В случае резонанса  . Для данной схемы справедливо следующее равенство:

Rвых=;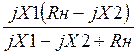

Разделяя равенство на вещественную и мнимую части и учитывая равенство   , получим: Rвых*Rн= Х1* Х1 ;  jX1Rн=0, откуда

X1=

Простейшие схемы, удовлетворяющие указанным условиям, представляют собой одноконтурные цепи согласования с включением нагрузки в емкостную или индуктивную ветвь

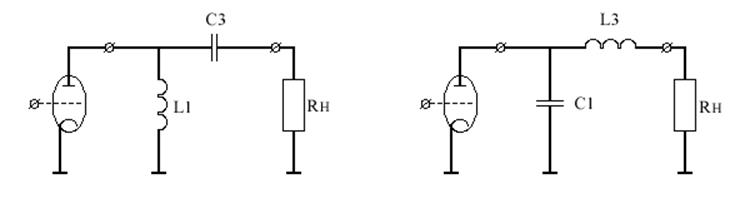
a)                                                                          б)    

Рис.2

Выразим общепринятые параметры контуров – характеристическое сопротивление р , сопротивление потерь Rп, добротность с нагрузкой Qн и резонансное сопротивление Rн – через:  и Gп:

Rп=1/Gп;  Qн=/Rн;  Rрез=1/Gн=.

Сравним коэффициенты фильтрации для двух простейших схем.

Результаты расчета а) 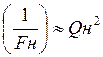, б) 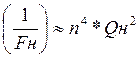 .                                                    говорят о том, что мощность гармоники в нагрузке, включенной в емкостную ветвь окажется в  раз больше мощности гармоники в нагрузке, включенной в индуктивную ветвь контура. Для улучшения фильтрации можно применить усложненные одноконтурные цепи согласования. Кроме того, при регулировке Gн в схемах нужно одновременно изменять В1 и В3 , что неудобно. Желательно регулировать Gн  не перестраивая контур. Такая возможность появляется с усложнением одноконтурных цепей согласования с частичным подключением лампы к контуру.

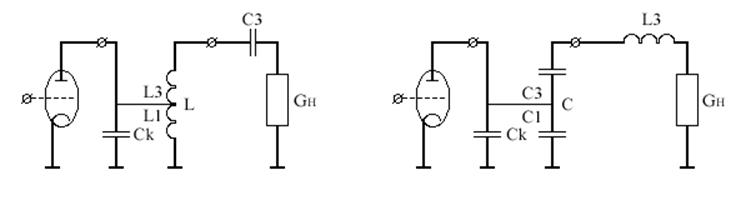
a)                                                                          б)    

Рис.3

В них удается увеличить, на сколько это возможно из конструктивных соображений, характеристические сопротивления контура р не меняя проводимостей В1 и В3. Поскольку  Rн=1/Gн задано, добротность Qн возрастает и фильтрация увеличивается.

Степень связи лампы с контуром характеризуется коэффициентом включения

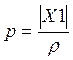, где , L=L1+L2, p=L1/L и 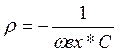, , 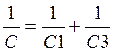p=C/C1.

Поэтому изменяя  при постоянных L и С1 можно, не расстраивая контур, регулировать нагрузку активного элемента

Rн=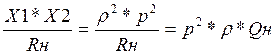

и добиться выполнения равенства Rн=Rн.кр.

Так обстоит дело, если не учитывать выходной емкости лампы Сак. Изменение ее включения в контур будет влиять на настройку, но на не слишком высоких частотах это влияние мало, и расстройку можно устранить, изменив L или С .

4.2. Сложная схема выхода.

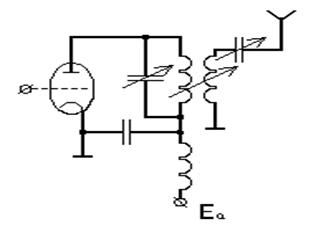
Рис.4

С изменением связи между контурами изменяется вносимое                                                                                                        сопротивление из антенного контура в промежуточный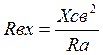 

Хсв - сопротивление связи между контурами, Ra - полное сопротивление антенны в контуре.

Эквивалентное сопротивление нагрузки в анодной цепи:

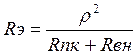
Оно увеличивается с уменьшением связи, т.к. уменьшается Rвн. В предельном случае

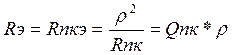
Допустим, что при отсутствии связи между контурами генератор находился в ПР. Тогда с увеличением связи Rэ генератора будет уменьшаться, и генератор постепенно будет переходить недопустимый режим

, .

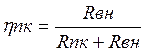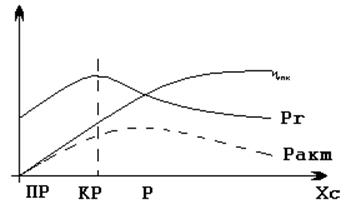
4.3. Расчёт критического режима АЭ при гармоническом    

 напряжении на выходе.

Исходными данными для расчета УМ являются рабочая частота f , мощность в фидере Рср, напряжение питания коллектора Еп, угол отсечки , параметры статических характеристик (S,Sкр,Sвх,E’,Eвх’), граничные частоты, характеристики влияния выходного напряжения на входное, максимально допустимые параметры Iвых макс,Uвх макс,Pрас макс. Цель расчёта – найти все напряжения, токи, мощности и другие параметры АЭ, работающего в критическом режиме, при условии получения заданной полезной выходной мощности Рвых=Р1кр.

Цепь коллектора для безинерционных и инерционных АЭ рассчитывается одинаково. Сначала по Рф выбирается Рвых: Рвых=(1,1…2)Рф, причем больший запас соответствует более сложным цепям согласования. Расчет начинаем с определения коэффициента использования коллекторного напряжения КР.

.

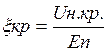Уравнение для кр найдём из формулы Р1=0,5*Uн*Iвых  Uн=Uн.кр=, , .

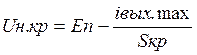отсюда iвых.max= или  тогда  .

Решая уравнение относительно , имеем

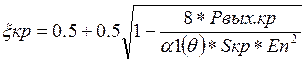
Второй корень уравнения соответствующий режиму с малым  и поэтому его отбрасываем. Затем вычисляем  и проверяем неравенство  

Далее находим 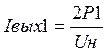 и по Iвых1 при выбранном , определяем высоту импульсов тока iвых.max и постоянную составляющую Iко  .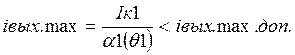

Рассчитаем потребляемую мощность Р0, мощность рассеваемую коллектором Ррас и электронный КПД: , , .

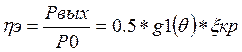Для реализации расчётного критического режима необходимо следующее сопротивление нагрузки выходной цепи АЭ: Rн=Uн.кр/Iвых1.

Расчёт характеристик цепи возбуждения усилителя мощности различен для без- и инерционных АЭ.

Для безинерционных АЭ примем следующий порядок расчета:

1) Uвх1=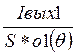; с учётом поправки на проницаемость D:

Uвх1=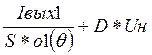, Ес=

Если в АЭ задано ограничение на обратное напряжение , то нужно проверить выполнение неравенства Uэб<Uэб.max.

2) Применяя аппроксимацию, определяем угол отсечки входного тока

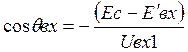
амплитуду первой гармоники Iвх1 и Iвхо

     

3) Далее вычисляем мощности, отдаваемые источником возбуждения, источником смещения и рассеиваемую на входе АЭ.

      Рвх1=0.5*Uвх*Iвх1     ,     Рсо=Ес*Iвхо     ,     Рвх.рас=Рвх1+Рсо.

Величину Рвх.рас в лампах нужно сравнить с допустимой мощностью потерь на управляющей сетке Рс1.max , а в транзисторах Рвх.рас нужно добавить к Ррас коллектора и проверить условие Ррас+Рвх.рас<Ррас.max.

4) Находим коэффициент усиления по мощности: Кр=Рвых/Рвх1.

5) Завершаем расчет определением необходимого для расчета предыдущего каскада среднего входного сопротивления АЭ по первой гармонике: Rвх=Uвх/Iвх.