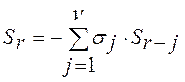 , где
, где ![]() -
количество произошедших ошибок;
-
количество произошедших ошибок; ![]() и перестраивает свою
структуру в зависимости от возможной ошибки в структуре формируемого сигнала.
и перестраивает свою
структуру в зависимости от возможной ошибки в структуре формируемого сигнала.
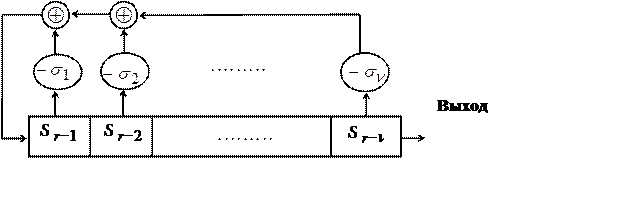 |
Для нахождения полинома
локатора ошибок используется итерационная процедура. На каждой итерации
вычисляется модель регистра с обратными связями, генерирующего первые r компонентов синдрома, где r – номер этапа. Длина регистра на r-м этапе обозначается ![]() . На r-м этапе оценка
. На r-м этапе оценка ![]() r-й компоненты синдрома равна:
r-й компоненты синдрома равна:
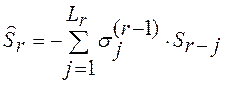 , где
, где 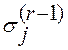 -
весовые коэффициенты на
-
весовые коэффициенты на ![]() -м предыдущем этапе.
-м предыдущем этапе.
Ошибка (невязка)
вычислений ![]() определяется как
определяется как
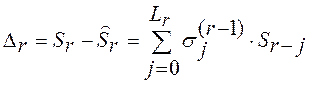 .
.
Если ![]() , то параметры модели не меняются
, то параметры модели не меняются
![]() .
.
Если ![]() , то параметры модели меняются по правилу
, то параметры модели меняются по правилу
![]() , где
, где ![]() - веса;
- веса;
![]() - некоторое целое число;
- некоторое целое число; ![]() - элемент поля.
- элемент поля.
Новая невязка может быть вычислена как
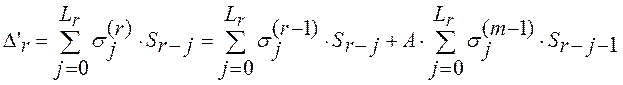 .
.
Определим величины ![]() так, чтобы новая
невязка
так, чтобы новая
невязка ![]() была равна нулю. Выберем следующие значения
была равна нулю. Выберем следующие значения
![]() так, чтобы
так, чтобы ![]() и
и ![]() . После подстановки получаем, что
. После подстановки получаем, что 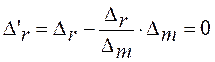 . В этом случае новая модель регистра
сдвига будет генерировать последовательность
. В этом случае новая модель регистра
сдвига будет генерировать последовательность ![]() . Если
выберем
. Если
выберем ![]() , то получим регистр с обратной связью
минимальной длины.
, то получим регистр с обратной связью
минимальной длины.
Теорема
Берлекэмпа –Месси.
Пусть заданы компоненты синдрома ![]() из некоторого поля,
тогда при начальных условиях
из некоторого поля,
тогда при начальных условиях ![]() ;
; ![]() ;
; ![]() выполняются
следующие рекуррентные равенства, использующиеся для вычисления
выполняются
следующие рекуррентные равенства, использующиеся для вычисления ![]() : 1.
: 1. 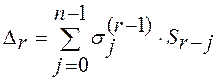 ;
;
2. ![]() ;
;
3. 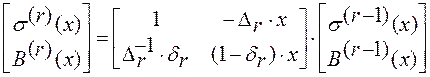 ,
,
где ![]() и
и 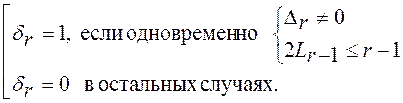 .
.
При выполнении таких условий полином ![]() является
многочленом наименьшей степени, коэффициенты которого удовлетворяют равенству
является
многочленом наименьшей степени, коэффициенты которого удовлетворяют равенству
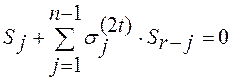 ,
где
,
где ![]() .
.
Граф-схема алгоритма Берлекэмпа–Месси приведена на рис. 2.
Процедура Ченя. Для вычисления инверсии корней
полинома ошибок удобно использовать следующий алгоритм. Воспользуемся тем
свойством, что сумма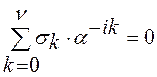 только в том случае, если
символ, располагающийся на
только в том случае, если
символ, располагающийся на ![]() -й позиции оказывается
ошибочным. Если определить
-й позиции оказывается
ошибочным. Если определить ![]() , тогда
, тогда ![]() , а
, а 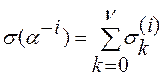 . В
итоге получается простая переборная схема вычислителя корней (рис.3).
. В
итоге получается простая переборная схема вычислителя корней (рис.3).
Рис. 3
Алгоритм
Форни.Позволяет оценить величины ошибок ![]() . Известно, что
. Известно, что 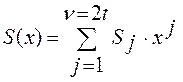 =
=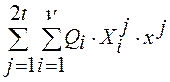 . Полином локатора ошибок имеет вид
. Полином локатора ошибок имеет вид 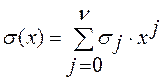 =
=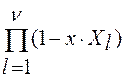 , где
, где ![]() - корни полинома. Составим ключевое
уравнение
- корни полинома. Составим ключевое
уравнение ![]() . Если в ключевое уравнение подставить
выражения для S(x), s(x) и решить его относительно
. Если в ключевое уравнение подставить
выражения для S(x), s(x) и решить его относительно ![]() , то получим оценку величины ошибки:
, то получим оценку величины ошибки:
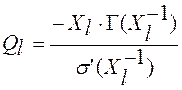
![]() , где
, где ![]() - формальная производная полинома.
- формальная производная полинома.
Пример. Троичный БЧХ-код (7, 3) формируется
над полем ![]() ,
, ![]() , для
которого
, для
которого ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Порождающий полином имеет вид
. Порождающий полином имеет вид
![]() .
.
Предположим, что на вход декодера поступает сигнал
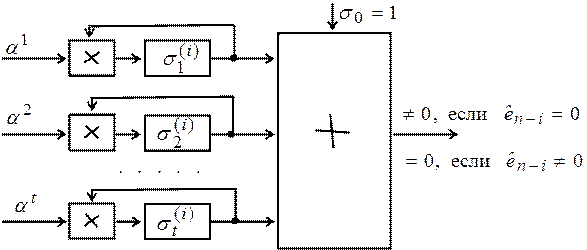 |
Алгоритм Берлекэмпа–Месси вычисляет полином локатора ошибок:
![]() ,
, ![]() , который имеет следующие корни:
, который имеет следующие корни: ![]() ,
, ![]() . Тогда
номера позиций ошибок определятся как 3 и 5. Ключевое уравнение запишется как
. Тогда
номера позиций ошибок определятся как 3 и 5. Ключевое уравнение запишется как
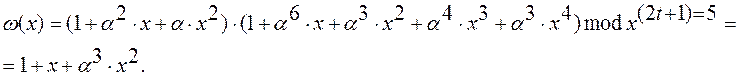
Откуда
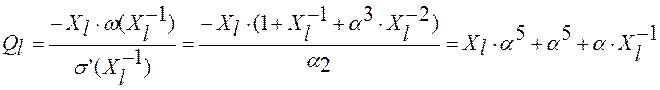 ;
;
![]() ;
; ![]() .
.
Оценка вектора ошибки
равна ![]() . Оценка кодового слова равна:
. Оценка кодового слова равна: ![]() .
.
2.4. Нумератор весов кода
Рассмотрим весовые характеристические функции линейного кода, содержащие полную информацию о структуре кода. Используются каналы, вносящие независимые ошибки в передаваемые символы с вероятностью p0 . Безошибочно символы принимаются с вероятностью (1 – p0).
Пусть задан линейный ![]() -код, символы которого
принадлежат q-ичному
множеству из
-код, символы которого
принадлежат q-ичному
множеству из ![]() , и пусть этот код содержит
, и пусть этот код содержит ![]() векторов веса i. Тогда совокупность чисел
векторов веса i. Тогда совокупность чисел ![]() называют
распределением весов, а многочлен
называют
распределением весов, а многочлен 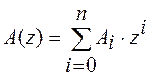 называют
характеристической функцией или нумератором весов кода C. На рис. 4 приведено распределение нумераторов веса для кода
БЧХ.
называют
характеристической функцией или нумератором весов кода C. На рис. 4 приведено распределение нумераторов веса для кода
БЧХ.
|
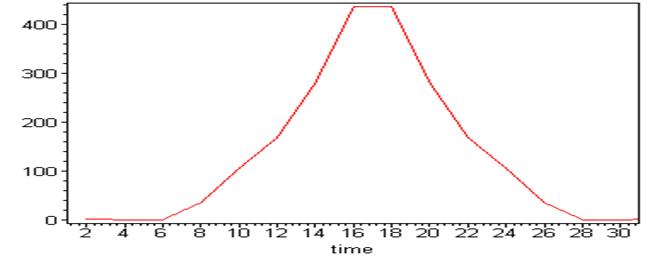
Рис. 4
Если выполняется неравенство 2t + 1 £ dmin и декодер исправляет все конфигурации ошибок, вес которых не превышает t, то вероятность ошибочного декодирования равна
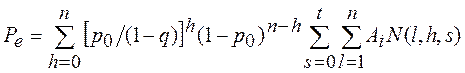 , где N(l, h, s) – число конфигураций ошибок веса h, находящихся на расстоянии s от кодового слова веса l.
, где N(l, h, s) – число конфигураций ошибок веса h, находящихся на расстоянии s от кодового слова веса l.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.