Для функции ошибки определим дискретное преобразование Фурье в конечном поле [ 4 ]
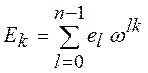 , k=1,…,2t.
, k=1,…,2t.
Заметим, что компоненты синдрома можно трактовать как коэффициенты Фурье
преобразования Sj = Ej, j= 1,…, 2t при ![]() .
.
Оценки параметров ошибки можно получить путем решения полученной
нелинейной системы уравнений, что достаточно сложно. Используем искусственный
приём. Введем так называемый полином локаторов ошибок ![]() :
:
![]() , или
, или
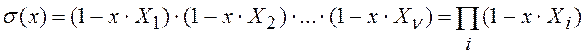 ,
,
нулям которого соответствуют элементы
![]() , l = 1,…,n.
, l = 1,…,n.
Корнями полинома ![]() являются величины
являются величины ![]() . Если коэффициенты
. Если коэффициенты ![]() известны,
то соответственно для определения локаторов ошибок
известны,
то соответственно для определения локаторов ошибок ![]() нужно
найти корни
нужно
найти корни ![]() , после чего вычислить обратные к ним
величины. При этом решение системы нелинейных уравнений сводится к решению
системы линейных уравнений относительно коэффициентов полинома
, после чего вычислить обратные к ним
величины. При этом решение системы нелинейных уравнений сводится к решению
системы линейных уравнений относительно коэффициентов полинома ![]() . Действительно, умножим левую и правую
части выражения для полинома локаторов ошибок на
. Действительно, умножим левую и правую
части выражения для полинома локаторов ошибок на ![]() , а
также положим, что при
, а
также положим, что при ![]() имеем
имеем ![]() .
Образуем систему
.
Образуем систему
![]() .
.
Просуммировав уравнения по индексу e от 1 до ![]() , для каждого индекса j получим:
, для каждого индекса j получим:
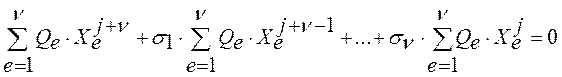 .
.
Учитывая, что
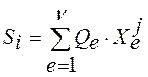 , система уравнений представляется в виде
, система уравнений представляется в виде
![]() ,
,
или в матричной форме:
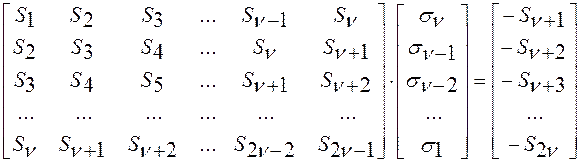
Система связывает компоненты синдрома ![]() с
коэффициентами полинома локаторов ошибок, задача вычисления которых решается
достаточно просто, если можно найти обратную матрицу синдромов.
с
коэффициентами полинома локаторов ошибок, задача вычисления которых решается
достаточно просто, если можно найти обратную матрицу синдромов.
2.3.1. Алгоритм Питерсона–Горенштейна–Цирлера (ПГЦ)
1.
Вычисляются
компоненты синдрома:![]() . Задается величина n = t.
. Задается величина n = t.
2.
Составляется
матрица синдромов ![]() , l,k = 0,1,…, n-1.
, l,k = 0,1,…, n-1.
3.
Вычисляется
определитель матрицы ![]() . Если
. Если ![]() ,
то матрица является сингулярной, и обратной матрицы не существует. В этом
случае изменяется размер матрицы n:= (n -
1) до тех пор, пока определитель не станет отличным от нуля. После чего
повторяется второй шаг.
,
то матрица является сингулярной, и обратной матрицы не существует. В этом
случае изменяется размер матрицы n:= (n -
1) до тех пор, пока определитель не станет отличным от нуля. После чего
повторяется второй шаг.
4. Определяются коэффициенты полинома локаторов ошибок:
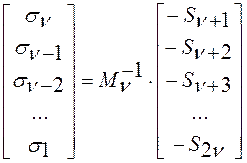
5. Определяются корни ![]() = 0 и через их инверсию вычисляют значения
= 0 и через их инверсию вычисляют значения
![]() .
.
6. Оцениваются величины ошибок ![]() , решая систему
, решая систему
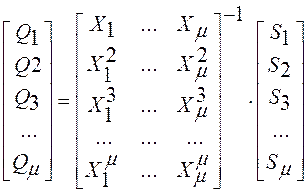
7. Корректируют принятый вектор, подставляя вычисленные значения Qi .
При количестве ошибок ![]() , данный алгоритм
характеризуется большой вычислительной сложностью. В этих случаях для
вычисления полинома локаторов ошибок используют алгоритмы Берлекэмпа–Месси,
Сугиямы, а для оценки значений ошибок для q-ичных кодов – алгоритм Форни .
, данный алгоритм
характеризуется большой вычислительной сложностью. В этих случаях для
вычисления полинома локаторов ошибок используют алгоритмы Берлекэмпа–Месси,
Сугиямы, а для оценки значений ошибок для q-ичных кодов – алгоритм Форни .
2.3.2. Алгоритм Сугиямы
Алгоритм Сугиямы позволяет решить систему уравнений в поле F
![]()
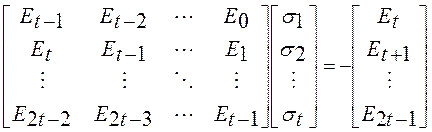 , что разрешает центральную проблему
декодирования локаторов ошибок.
, что разрешает центральную проблему
декодирования локаторов ошибок.
Предполагаем, что ![]() , полином локаторов ошибок
, полином локаторов ошибок 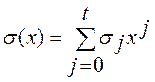 и полином спектральных коэффициентов
и полином спектральных коэффициентов![]() функции ошибок
функции ошибок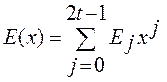 .
Считается, что коэффициенты полинома произведения
.
Считается, что коэффициенты полинома произведения ![]() равны
нулю для j = t,…,2t-1.
равны
нулю для j = t,…,2t-1.
Решение матричной системы
уравнений эквивалентно решению полиномиального уравнения ![]() для степени полинома
для степени полинома ![]() не больше, чем t, и степени
не больше, чем t, и степени ![]() не
больше, чем t – 1.
не
больше, чем t – 1.
Рассматриваемый алгоритм решает полиномиальное
уравнение с использованием алгоритма Евклида следующим образом. Обозначим
начальные условия как ![]() и
и ![]() .
Верхний индекс обозначает номер итерации (этапа) алгоритма. Для r - й
итерации вычисления алгоритма Евклида можно записать
.
Верхний индекс обозначает номер итерации (этапа) алгоритма. Для r - й
итерации вычисления алгоритма Евклида можно записать
![]() при
при ![]() .
.
Определим условие
выполнения равенства ![]() :
:
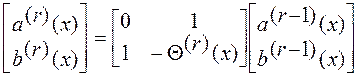 .
.
Матрицу ![]() r - й итерации по индукции можно определить как
r - й итерации по индукции можно определить как
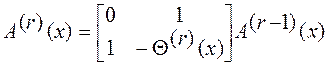 и
и 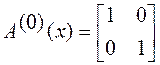 .
.
Для ![]() имеем
имеем
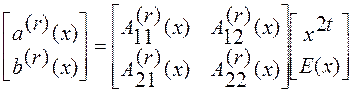 .
.
Откуда получаем желаемую форму уравнения
![]() ,
, ![]() .
.
Для решения задачи
декодирования требуется найти такое значение r, при котором ![]() и
и ![]() . Это требование удобно выполнить, выбирая rt как значения r, удовлетворяющие условиям
. Это требование удобно выполнить, выбирая rt как значения r, удовлетворяющие условиям ![]() и
и ![]() .
.
2.3.3. Алгоритм Берлекэмпа–Месси
Позволяет найти полином локаторов ошибок. В основе алгоритма лежит адаптивная авторегрессионная модель генератора (рис.1), который формирует компоненты синдрома по правилу:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.