Решение систем линейных алгебраических уравнений. Метод исключения Жордана и его модификация, страница 4

void Calculate()                                      //функция нахождения решений

{

int i, j, k;                                                //задание переменных

double t;              

for(i = 0; i < n-1; i++)                            //непосредственно алгоритм

for(j = i+1; j < n; j++)               

if(t = a[j][i])

{                                                                                   //изменние элементов                                                                                 for(k = i; k < n; k++)                                        //матрицы А и столбца B

a[j][k] = a[i][i] * a[j][k] / t - a[i][k];     //по соответствующим 

b[j] = a[i][i] * b[j] / t - b[i];                              //формулам метода

}

for(i = 0; i < n; i++)

if(t = a[i][i])

{

for(j = i; j < n; j++)

a[i][j] /= t;

b[i] /= t;

}

for(i = n-1; i; i--)

for(j = i-1; j >= 0; j--)                                    //вынесение решений в столбец B

b[j] -= a[j][i] * b[i];                                                       

}

void AllocVars()                                                          //функция аллокирования памяти                                                            

{

a = new double*[n];                                                   //выделение памяти под массивы

for(int i = 0; i < n; i++)

a[i] = new double[n];

b = new double[n];

}

void FreeVars()                                                             //функция освобождения памяти

{

for(int i = 0; i < n; i++)                                                //освобождение памяти, выделенной  

delete[] a[i];                                                               //под массивы

delete[] a;

delete[] b;

}

bool ReadData()                                                           //функция считывания из файла

{

int i,j;

char p[200];

printf("Please enter file name:\n");                             //ввод имени файла, в котором

scanf("%s",p);                                                             //находится решаемая система

FILE *fIn = fopen(p, "r");                                           //открытие этого файла

if(!fIn) return false;

fscanf(fIn, "%d", &n);                                                

AllocVars();                                                                //вызов функции аллокирования памяти

for(i = 0; i < n; i++)                                                     //считывание матриц из файл в

for(j = 0; j < n; j++)                                                 //созданные массивы  

fscanf(fIn, "%lf", &a[i][j]);

for(i = 0; i < n; i++)

fscanf(fIn, "%lf", &b[i]);

return true;

}

5.  Результаты вычислений

Исходные данные:

;              

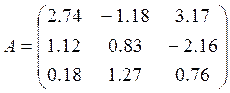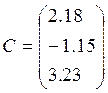
Метод Гаусса:

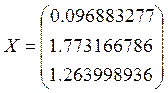
Метод Жордана:

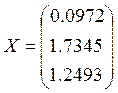
Сравнивая результаты вычислений, приходим к выводу, что метод Гаусса обладает большей точностью, но при этом метод Жордана более удобен тем, что в нём не приходиться пошагово находить каждое решение системы – они  явно выражаются через столбец C  .

6. Список литературы

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы, М. 1987.

2. Крылов В.И., Бобков В.В., Монастырский П.И. Вычислительные методы, т.1, М. 1976

3. Фадеев, Фадеева. Вычислительные методы линейной алгебры.

4. Амосов А.А. и др. Вычислительные методы для инженеров, М. 1994.

5. Форсайд Дж., Молер К. Численное решение систем линейных алгебраических             уравнений, М. 1969.

6. Воеводин. Численные методы алгебры. Теория и алгоритмы.

7. Самарский А.А. Введение в численные методы.