нормально распределенных генеральных совокупностей с разными значениями параметров. По объединенной выборке, моделирующей выборку из конечной смеси двух распределений, составлен вариационный ряд.
Найдены выборочные характеристики:
|
наибольшее значение (МАКС) |
2,375654731 |
|
наименьшее значение (МИН) |
-3,046006896 |
|
объем выборки (СЧЕТ) |
60 |
|
выборочную среднюю (СРЗНАЧ) |
0,006933552 |
|
медиана (МЕДИАНА) |
-0,084900762 |
|
мода (МОДА) |
#Н/Д |
|
вариационный размах |
5,421661626 |
|
исправленная выборочная дисперсия (ДИСП) |
1,313330188 |
|
дисперсия (смещенная) выборки (ДИСПР) |
1,291441351 |
|
выборочное среднее квадратическое отклонение (СТАНДОТКЛОН) |
1,14600619 |
|
выборочное среднее квадратическое отклонение (СТАНДОТКЛОНП) |
1,136416011 |
|
среднее абсолютное отклонение от выборочного среднего (СРОТКЛ) |
0,916297696 |
|
эксцесс эмпирического распределения (ЭКСЦЕСС) |
-0,13075382 |
|
асимметрия эмпирического распределения (СКОС) |
-0,225034651 |
|
коэффициент вариации |
1,652841461 |
|
ошибка выборки |
0,147948763 |
Медиана - значение, которое делит вариационный ряд на две равные (по числу значений) части.
Мода - наиболее часто встречающееся значение.
Вариационный размах ![]() (размах выборки) - разница между
наибольшим и наименьшим значениями выборки.
(размах выборки) - разница между
наибольшим и наименьшим значениями выборки.
Эксцесс эмпирического распределения - значение, характеризующее форму кривой распределения.
Асимметрия эмпирического распределения - значение, характеризующее форму кривой распределения.
Коэффициент вариации, равен выборочному среднему квадратическому отклонению, деленному на выборочную среднюю.
Ошибка выборки, равна среднему квадратическому отклонению, деленному на корень из числа наблюдений.
|
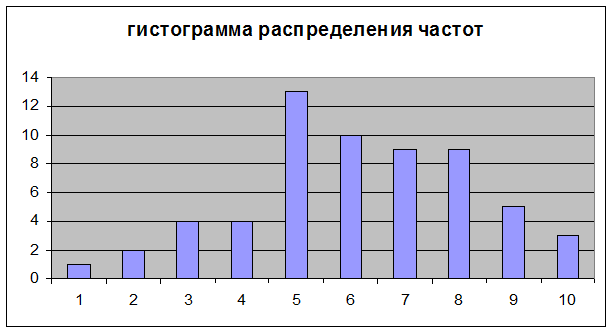
№ интервала |
правая граница |
середина интервала |
частота |
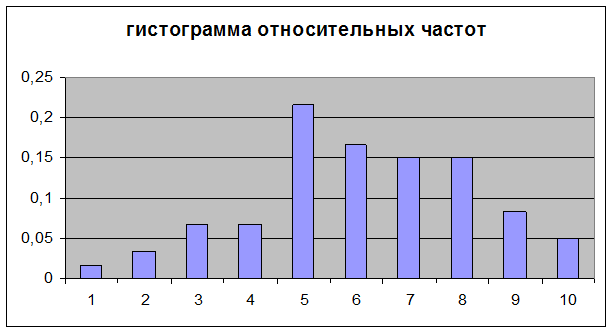
относительная частота |
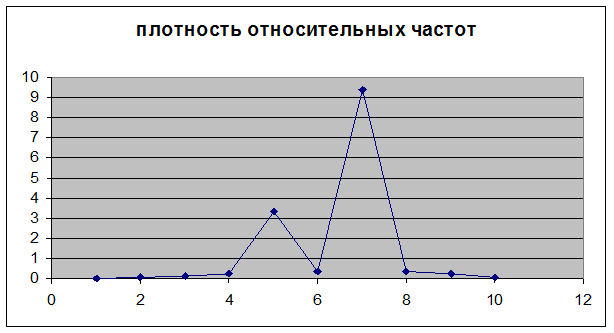
плотность относительной частоты |
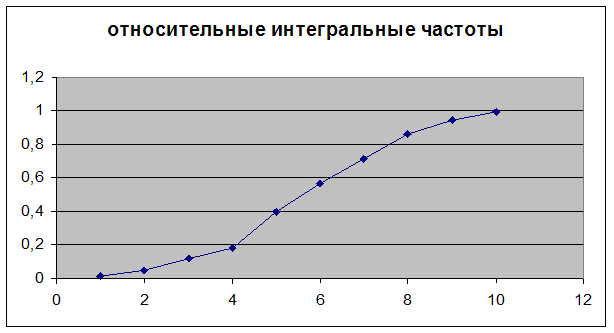
интегральная частота |
относительные кумулятивные частоты |
|
|
1 |
-2,5038 |
-2,774923 |
1 |
0,0166667 |
0,012467984 |
1 |
0,016666667 |
|
|
2 |
-1,9616 |
-2,232757 |
2 |
0,0333333 |
0,0807593 |
3 |
0,05 |
|
|
3 |
-1,4195 |
-1,690591 |
4 |
0,0666667 |
0,140165166 |
7 |
0,116666667 |
|
|
4 |
-0,8773 |
-1,148425 |
4 |
0,0666667 |
0,232972675 |
11 |
0,183333333 |
|
|
5 |
-0,3351 |
-0,606259 |
13 |
0,2166667 |
3,35207133 |
24 |
0,4 |
|
|
6 |
0,20699 |
-0,064093 |
10 |
0,1666667 |
0,372676328 |
34 |
0,566666667 |
|
|
7 |
0,74916 |
0,4780732 |
9 |
0,15 |
9,402893054 |
43 |
0,716666667 |
|
|
8 |
1,29132 |
1,0202393 |
9 |
0,15 |
0,347358626 |
52 |
0,866666667 |
|
|
9 |
1,83349 |
1,5624055 |
5 |
0,0833333 |
0,250493036 |
57 |
0,95 |
|
|
10 |
2,37565 |
2,1045716 |
3 |
0,05 |
0,045488406 |
60 |
1 |
Относительная
частота ![]() равна значению соответствующей частоты,
деленной на число элементов выборки
равна значению соответствующей частоты,
деленной на число элементов выборки 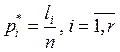 . Сумма значений
полученных относительных частот должна быть равна 1.
. Сумма значений
полученных относительных частот должна быть равна 1.
Плотность
относительной частоты равна значению относительной частоты, деленной на
длину интервала разбиения: 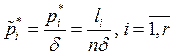 .
.
Значение кумулятивной
частоты для интервала представляет собой сумму частот текущего и всех
предыдущих интервалов (накопленные частоты): 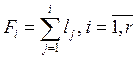 .
.
Относительные
кумулятивные частоты равны кумулятивным частотам, деленным на число
элементов выборки: 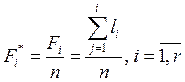 .
.
Лабораторная работа № 2
Основы обработки статистических данных на Excel: Корреляция.
Задание:
1. Смоделируйте две выборки из 60 значений нормально распределенных случайных величин. Получите еще одну выборку из 60 нормально распределенных значений с помощью стандартных средств Excel.
2. Вычислите: выборочные коэффициенты корреляции для всех трех полученных выборок, выборочные ковариации для пар выборок, средние квадратические отклонения для выборок. И проверьте по формуле парного коэффициента корреляции полученные ранее с помощью функции Excel значения коэффициентов корреляции.
3. Постройте корреляционную матрицу размерности 3*3 с помощью стандартных средств Excel.
Результаты:
Смоделировано две выборки из 60 значений нормально распределенных случайных величин. С помощью стандартных средств Excel получена еще одна выборка из 60 нормально распределенных значений.
|
выборочные коэффициенты корреляции (ПИРСОН) |
||
|
1 |
2 |
3 |
|
-0,065626214 |
-0,066935129 |
-0,192692609 |
|
выборочные ковариации (КОВАР) |
||
|
1 |
2 |
3 |
|
-0,268480784 |
-0,042734742 |
-0,113446051 |
|
средние квадратические отклонения (СТАНДОТКЛОНП) |
||
|
1 |
2 |
3 |
|
1,942301317 |
2,106295285 |
0,303115204 |
|
парный коэффициент корреляции |
||
|
1 |
2 |
3 |
|
-0,065626214 |
-0,066935129 |
-0,192692609 |
|
выборочные дисперсии |
||
|
1 |
2 |
3 |
|
3,772534405 |
4,436479828 |
0,091878827 |
|
корреляционная матрица |
|||
|
Столбец 1 |
Столбец 2 |
Столбец 3 |
|
|
Столбец 1 |
1 |
||
|
Столбец 2 |
-0,065626214 |
1 |
|
|
Столбец 3 |
-0,192692609 |
-0,066935129 |
1 |
Лабораторная работа № 3
Интервальное оценивание:
Интервальная оценка параметров распределения. Доверительные интервалы.
Задание:
1. Смоделируйте генеральную совокупность из 100 значений
нормально распределенной случайной величины. Запишите использованные при этом
значения математического ожидания ![]() и среднего
квадратического отклонения
и среднего
квадратического отклонения ![]() . Постройте гистограмму
и полигон относительных частот для смоделированной генеральной совокупности
(для 7 и 10 интервалов разбиения).
. Постройте гистограмму
и полигон относительных частот для смоделированной генеральной совокупности
(для 7 и 10 интервалов разбиения).
2. Вычислите дисперсию ![]() и
среднее квадратическое отклонение
и
среднее квадратическое отклонение ![]() полученной генеральной
совокупности, математическое ожидание смоделированной генеральной совокупности
полученной генеральной
совокупности, математическое ожидание смоделированной генеральной совокупности ![]() , вероятность попадания случайной величины
, вероятность попадания случайной величины ![]() в интервал
в интервал
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.