Цифровая фильтрация сигналов. Общие сведения о фильтрации сигналов, описание программного обеспечения проектирования и функционирования фильтров, задания на лабораторные работы, примеры решения характерных модельных задач нерекурсивной и рекурсивной фильтрации

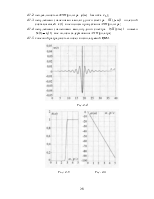
компактная таблица с реализацией отсчетов АЧХ , а также фиксируется значение параметра L.

Исследуется влияние на параметр L неравномерности в полосе задерживания  ([0,0001; 0,0500]), параметра  ([1,05; 2,50]), шага  ([0,05 с; 0,25 с]) и коэффициента усиления  ([0,1; 10,0]). Для этого указанные параметры по одному варьируются в заданных пределах. Достаточно задать по 10 примерно равноотстоящих значений для каждого из параметров, включая границы диапазона. При этом остальные параметры задаются аналогично базовому варианту, т.е. одновременно изменяться может только один исследуемый параметр! Приводятся таблицы и графики, иллюстрирующие полученные зависимости.

Дополнительно построить:

§  график АЧХ для базового варианта, задав =150 р/с;

§  график АЧХ для базового варианта, задав =1 с.

Таким образом, в отчете должны содержаться 9 графиков и 5 таблиц. Иметь в виду, что графики и таблицы понадобятся при выполнении л.р. №2.

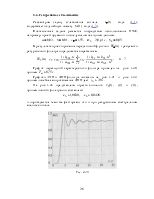
Делаются выводы о соответствии параметров спроектированного фильтра заданным требованиям посредством определения по реализации отсчетов АЧХ полученных значений параметров для базового варианта и сравнения их с исходными данными. Также поясняется характер полученных для параметра L зависимостей, например:

Выводы:

1.  Спроектирован низкочастотный фильтр со следующими параметрами АЧХ: =1,0 при заданном 1,0; =2,1 р/с при заданном 2,0 р/с; =0,45 р/с при заданном 0,5 р/с; 0,008 при заданном 0,01. Таким образом, фильтр в целом удовлетворяет заданным параметрам. Параметр L для базового варианта равен 256.

2.  Зависимости параметра L от неравномерности , параметра  и шага  имеют монотонный характер, причем с уменьшением указанных параметров значение L возрастает. Это объясняется тем, что…

3.3. Лабораторная работа № 2. Функционирование  нерекурсивного  фильтра

Приводятся исходные данные в соответствии с вариантом из табл. 1, а также общие для всех вариантов. Приводить данные, не имеющие отношения к выполняемой работе, не нужно.

Дается описание модельной задачи, включающее полную информацию об обрабатываемых сигналах.

Приводятся расчетные соотношения функционирования фильтра.

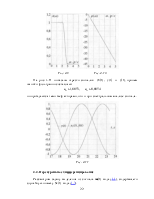
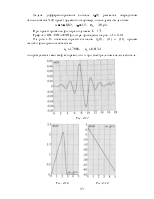
Для базового варианта приводятся графики ИХ, АЧХ и ФЧХ фильтра, значение параметра L (можно взять из л.р. №1).

Исследуется влияние на ошибки фильтрации  и  неравномерности  ([0,0001; 0,0500]), параметра  ([1,05; 2,50]), шага  ([0,05 с; 0,25 с]). Для этого указанные параметры по одному варьируются в заданных пределах. Достаточно задать по 10 примерно равноотстоящих значений для каждого из параметров, таких же, как и в л.р. №1, т.к. потребуется использовать полученные ранее значения L для каждого из параметров. При этом остальные параметры задаются аналогично базовому варианту, т.е. изменяться может только один исследуемый параметр! Приводятся таблицы (сводные по ошибкам, содержащие данные из л.р. 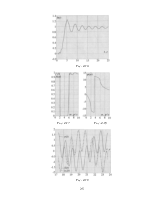№1) и графики, иллюстрирующие полученные зависимости. Зависимости ошибок фильтрации  и  для каждого исследуемого параметра строить на одном графике.

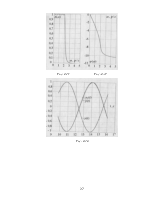
Также для базового варианта приводятся график сигнала  и графики сигналов   (все три на одном графике).

Таким образом, в отчете должны содержаться 8 графиков и 3 таблицы.

По графику ФЧХ определяется значение величины фазовой задержки .

Делаются выводы о соответствии полученных результатов условиями модельной задачи на основе полученных графиков сигналов. Также поясняется характер полученных для ошибок  и  зависимостей. Приводится полученная по графику ФЧХ величина фазовой задержки и делается вывод о возможностях устранения фазовой погрешности. Указываются составляющие ошибок нерекурсивной фильтрации