Классификация фильтров. Типы фильтров по частотным характеристикам. Исходные данные при проектировании фильтров на примере АЧХ спроектированного в ходе лабораторной работы фильтра. Характеристики нерекурсивных фильтров. Виды нерекурсивных фильтров. Оптимальные фильтры с минимаксной ошибкой (общие положения)

1 Классификация фильтров

Функционирование автоматических и автоматизированных систем управления и контроля технологическими процессами и техническими объектами непременно сопровождается разнообразной обработкой измеряемых реализаций сигналов. При этом очень часто возникает необходимость решения следующих задач:

-  спектральный анализ сигнала, т.е. выделение совокупности гармонических составляющих определенного диапазона частот; сглаживание сигнала, т.е. уменьшение в реализации сигнала уровня высокочастотных составляющих аддитивной помехи;

-  сглаживание сигнала, т.е. уменьшение в реализации сигнала уровня высокочастотными составляющими.

-  дифференцирование сигнала, зашумленного аддитивной помехой с высокочастотными составляющими.

Указанные и другие задачи решаются путем применения различных линейных фильтров, представляющих собой линейные динамические звенья. В зависимости от характера обрабатываемого сигнала различают следующие фильтры (см. рис. 1.1):

- 
непрерывные фильтры (на входе и выходе действуют непрерывные сигналы    и  ;

-  дискретные фильтры (на входе и выходе действуют дискретные сигналы    и  ,    – шаг дискретизации по времени,  ,  которые разделяются на рекурсивные и нерекурсивные.

В современных условиях дискретные фильтры реализуются на основе специализированных цифровых вычислительных устройств, микро- или мини-ЦВМ. При этом возникает эффект конечной разрядности чисел и такие дискретные фильтры принято называть цифровыми.

Математической моделью непрерывного фильтра является линейное дифференциальное уравнение  -го порядка

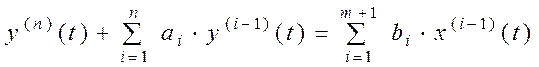,    ,   (1.1)

или соответствующая ему передаточная функция

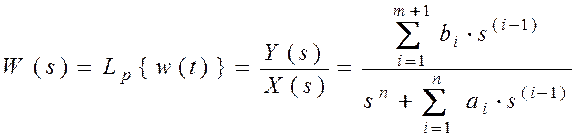, где   – переменная непрерывного преобразования Лапласа,

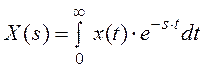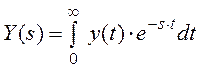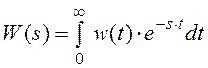,  ,  , а   – импульсная характеристика фильтра.

Другой формой математической модели непрерывного фильтра может служить интегральное уравнение свертки

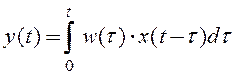.                                     (1.2)

Математической моделью рекурсивного фильтра является линейное разностное уравнение -го порядка

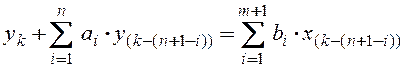,   ,                (1.3)

представляющее собой дискретный аналог дифференциального уравнения (1.1), или соответствующая уравнению (1.3) передаточная функция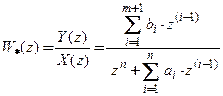, где    – переменная  Z -преобразования,  ,

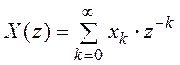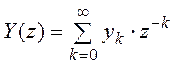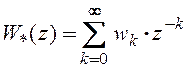,    ,    , а   – импульсная характеристика фильтра.

Математической моделью нерекурсивного фильтра служит дискретная форма интегрального уравнения свертки (1.2) –

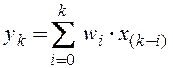, причем импульсная характеристика нерекурсивного фильтра является финитной, т.е. имеет конечную длительность –

     при     ,         при     , и его передаточная функция записывается в виде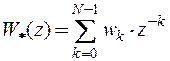

.                                           (1.4)

2 Типы фильтров по частотным характеристикам

Частотные характеристики непрерывных фильтров являются непериодическими функциями частоты    и определяются на интервале  .  Частотные характеристики дискретных фильтров представляют собой периодические с периодом  ,  ,  функции частоты  ,  в результате чего они полностью определяются на интервале  .

В зависимости от характера обработки входного сигнала фильтры обладают различными амплитудными частотными характеристиками (АЧХ). При этом могут быть выделены четыре основных типа фильтров: низкочастотный (НЧФ), полосовой (ПФ), режекторный (РФ) и высокочастотный (ВЧФ) фильтры, а также представляющий значительный практический интерес дифференцирующий фильтр (ДФ). Идеализированные АЧХ данных дискретных фильтров в интервале частот    приведены на рис. 1.2  1.6 соответственно.

         

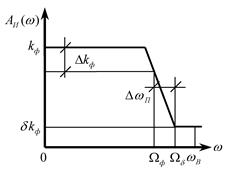
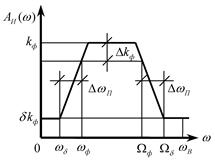
Рис. 1.2.                                                               Рис. 1.3.

 

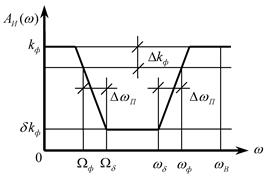
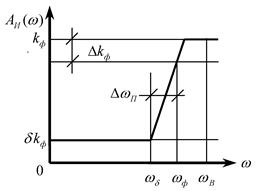
Рис. 1.4.                                                                                                      Рис. 1.5.

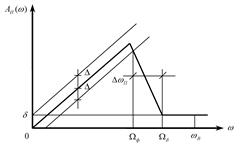 На каждой АЧХ выделяются полосы:

1)  полоса пропускания для НЧФ и ДФ                    , для ПФ                                 , для РФ                                  и ,

для ВЧФ                              ;

2)  переходная полоса для НЧФ и ДФ                    , для ПФ                                  и

для РФ                                  и ,

для ВЧФ                             

3)  полоса задерживания для НЧФ и ДФ                    , для ПФ                                                      и

для РФ                                                     , для ВЧФ                              .

Рис.1.6.

  и    – верхняя и нижняя граничные частоты полос пропускания,

  и    – верхняя и нижняя граничные частоты переходных полос.

Качество фильтра определяется относительными (относительно коэффициента усиления фильтра  ) неравномерностями его АЧХ в полосах пропускания (неравномерность  )  и полосах задерживания (неравномерность  ),  а также шириной переходных полос (для НЧФ, ВЧФ и ДФ –  ),  для ПФ и РФ -  ).  Ширину    переходных полос АЧХ удобно характеризовать относительным параметром    в виде:

для НЧФ

для РФ

для ПФ

для ВЧФ

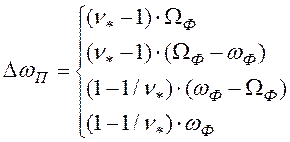                                                                                        (1.5)

С увеличением параметров  ,    и    качество фильтра ухудшается.

В заключение отметим два характерных режима фильтрации:

1)  режим реального времени, при котором для вычисления выходного