Заметки и краткие ответы на экзаменационные вопросы по дисциплине "Представление знаний в интеллектуальных системах", страница 2

1)  "Y $X отец (X,Y) у каждого человека есть хотя бы один отец

2)  $X "Y отец (X,Y) один отец для всех

Правильно построенная формула (ППФ).

ППФ – это логическая формула, состоящая из комбинации логических связок и кванторов.

Логические формулы строятся по следующим правилам:

1)термом является константа (переменная), либо картеж из множества термов, перед которым стоит функтор.

2)предикат – это картеж из множества термов, перед которым стоит предикатный символ.

3)атомарный предикат является логической формулой.

   4)если F и G – логические формулы, то (F); F,G; FvG; F←G; F↔G; ךF – также логические формулы.

5)если F(X) – логическая формула, то  ("X) F(X) и ($X)F(X) – логические формулы.

6)все результаты, полученные повторением пунктов 1…5 являются логическими формулами.

Вопрос №6.

Логический вывод – это процесс получения из множества ППФ некоторой другой ППФ путём применения одного или нескольких правил вывода.

1)Правило резолюции простых предложений.

Оно применяется в простых формулах:

Факт:  А

Отрицание: ך()

Импликация (если): А←

где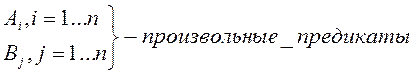

Пример:

Пусть имеются две правильно построенные формулы:

 ךA

 A←B

S: ךB

где А – предикат из формулы  совпадает с предикатом из формулы .

Предложения  и  называется родительским.

Результат вывода из   и  называется резольвента.

Данная резолюция соответствует правилу modus tollens:

ךA, A←B

      ךВ

Допуская, что: НЕ А и А если В

Выводим: НЕ В.

Пример:

Пусть   ךA

      A

     S: □ (пустое отрицание (противоречие)).

2)Правило резолюции для сложных предложений.

 ך()

 ←

где   - предикат, который совпадает в  и .

Резольвента получается путём подстановки .

S: ך()

Пример:

Допустим, что: НЕ (темно и зима и холодно)

и что: зима если январь

выводим: Не(темно и январь и холодно)

Пример:

 - факт, то есть :

В этом случае  вычёркивается из .

выводим: НЕ(темно и холодно)

Вопрос №7.

1)Простая резолюция сверху вниз.

Резолюция сверху вниз – это логический вывод, который порождает последовательность отрицаний.

Пример:

: получает (студент, стипендию) ←сдаёт (успешно, сессию, студент)

: сдаёт (успешно, сессию, студент)

Запрос: Получает ли студент стипендию?

: ך  получает (стипендию, студент)

В этом случае система должна опровергнуть это отрицание при помощи других предложений, показывая, что данное допущение ведёт к противоречию.

ШАГ 1 К предложениям  и  применяется правило modus tollens

ךA, A←B

      ךВ

допуская, что: Не получает студент стипендию и получает студент стипендию, если сдаёт успешно сессию.

выводим: не сдаёт успешно сессию студент

S: ך сдаёт (успешно, сессию, студент)

ШАГ 2 Берётся S и  и применяем правило  ךA,A

□

Допуская, что:

 ך сдаёт (успешно, сессию, студент) и сдаёт (успешно, сессию, студент)

Выводим:   □

Таким образом доказана противоречивость трёх формул , и .

Если считать, что  и  не противоречат друг другу, то они совместно противоречат .

ך : ך(ךполучает (студент, стипендию))

2)Общая резолюция сверху вниз.

: сдаёт (успешно, сессию, студент)

Запрос: Получает ли студент стипендию?

: получает (студент, Y)

: получает (X, стипендию) ←сдаёт (успешно, Z,X)

: получает (студент, стипендию) – общий пример родительских предикатов

Θ={X:=студент, Y:=стипендия}

Операция присваивания называется унификацией, а Θ – унификатором.

Вопрос №8.

Унификатор – это множество присваиваний следующего вида:

Θ={X:=,…,},

где  - переменная,

        - терм (наименьшая единица языка).

Применение X и t к двум выражениям даёт одинаково общие примеры.

Родительские предложения	Унификатор	Общий пример
P(7), P(7)	Θ - пустое	P(7)
P(X), P(57)	Θ={X:=5}	P(X)Θ=P(5)Θ=P(5)
P(X), P(Y)	Θ={X:=Y}	P(Y)
P(X,Y), P(5,X)	Θ={X:=5,Y:=X}={X:=5,Y:=5}	P(5,5)=P(X,Y)Θ= P(5,X)Θ=P(5,5)
ך P(5,X), P(X,Y) ←q(X)	Θ={X:=5,Y:=X}={X:=5,Y:=5}	ך q(X)Θ= ך q(5)

Решение задач с использованием логического программирования разбивается на три этапа:

1)формулируются знания и допущения по предметной области в виде правильно построенных формул.

2)составление допущений и запросов.

3)решение задачи от противного, то есть исходного отрицания путём порождения других отрицаний. Если может быть построен вывод, который заканчивается отрицанием, то этот вывод называется успешным выводом.

Вопрос №9.

Семантическая сеть – это система знаний в виде образа сети-узлы, который соответствует понятиям и объектам, а дуги отношениям между объектами.

Существует 2 типа отношений:

1)Отношения включения или совпадения – IS-А. Человек IS-А Млекопитающее.

Такие отношения имеют иерархическую структуру и обладают свойством наследования.

2)Отношение целое - часть: Part-OF. Нос Part-OF головы

Семантическая сеть представляется в виде диаграмм.

Факты:                                                           Наследование:

Вася – мужчина                                            Вася - животное

Мужчина - животное

Part-OF

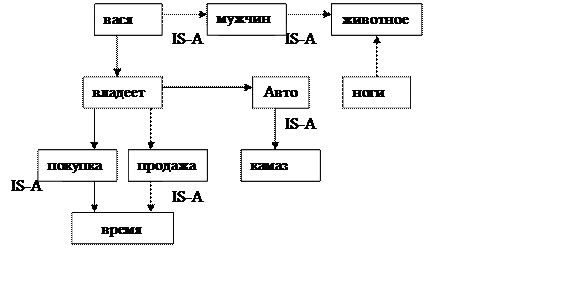
Семантическая сеть как Пролог программа.

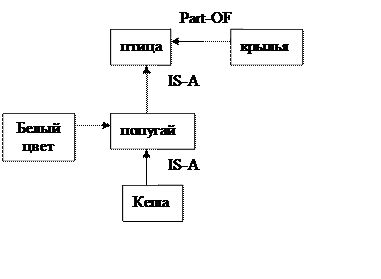
является (попугай, птица).

является (кеша, попугай).

имеет (белый цвет, попугай).

имеет (крылья, птица).

Имеет (X, Y):-

Является (Y, Z), имеет (X, Z).

Элементы семантической сети. (СС)

Семантическая сеть – это ориентированный граф с поименованными дугами и вершинами.

Вершины бывают 3 типов:

1)Понятия – это сведения об объектах предметной области.