Организация, проведение и обработка результатов активного эксперимента, страница 2

Для построения плана ДФЭ в качестве реплики берут план ПФЭ с меньшим числом факторов k. Число опытов n при этом должно быть не меньше числа коэффициентов линейного уравнения регрессии.

Таблица 3

Полу реплика ПФЭ типа 2⁴ или план ДФЭ.

	Факторы
	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9	Z10	Z11	Z12	Z13	Z14	Z15	Z16
№ опыта	X0	X1	X2	X3	X4	X1*X2	X1*X3	X1*X4	X2*X3	X2*X4	X3*X4	X1*X2 *X3	X1*X2*X4	X1*X3*X4	X2*X3*X4	X1*X2*X3*X4
1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
2	1	1	1	-1	-1	1	-1	-1	-1	-1	1	-1	-1	1	1	-1
3	1	1	-1	1	-1	-1	1	-1	-1	1	-1	-1	1	-1	1	-1
4	1	1	-1	-1	1	-1	-1	1	1	-1	-1	1	-1	-1	1	1
5	1	-1	1	1	-1	-1	-1	1	1	-1	-1	-1	1	-1	-1	-1
6	1	-1	1	-1	1	-1	1	-1	-1	1	-1	1	-1	-1	-1	1
7	1	-1	-1	1	1	1	-1	-1	-1	-1	1	1	1	1	-1	1
8	1	-1	-1	-1	-1	1	1	1	1	1	1	-1	-1	1	-1	-1

Заключение о воспроизводимости даётся на основе проверки гипотезы об однородности ряда дисперсий по критерию Кохрена

                                                                        (3)

где G – расчетная величина коэффициента Кохрена

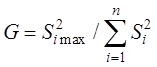;                                                                (4)

– оценки построчных дисперсий

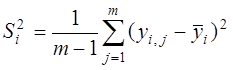;                                                 (5)

 – число дублированных опытов;  – среднее значение результата в каждой серии  дублированных опытов

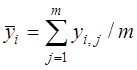;                                                                  (6)

– критерий Кохрена при доверительной вероятности p, числах степеней свободы и .

Статистическую значимость коэффициентов регрессии проверяют по критерию Стьюдента:

,                                                                      (7)

где t - коэффициент Стъюдента

;                                                                        (8)

 - дисперсия ошибки определения коэффициентов b_j, рассчитываемая при ортогональных планах по условию

,                                                                     (9)

а при неортогональном плане – как диагональные элементы ковариационной матрицы

;                                                            (10)

 - средняя дисперсия эксперимента

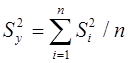.                                                                    (11)

Рассеяние результатов эксперимента вблизи уравнения, аппроксимирующего функциональную искомую зависимость, можно охарактеризовать с помощью дисперсии неадекватности, оценки которой рассчитывают по формуле

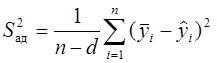,                                                  (12)

где d – число членов аппроксимирующего полинома.

Гипотезу об адекватности проверяют по критерию Фишера

.                                                             (13)

В случае если >, коэффициент Фишера определяется отношением

.                                                            (14)

При этом f₁ = n-d и f₂ = n(m-1). Если f₁ = 0, принимается f₁ = 1.

При  £  условие (19) выполняется для любого числа степеней свободы и уравнение регрессии адекватно эксперименту.